
【题目】综合与实践
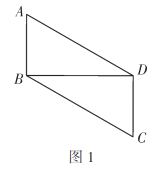
图形变换的基本方式有:平移变换、旋转变换、轴对称变换.在数学综合与实践课上,张老师将两块含![]() 角的全等三角尺按图1方式摆放在一起 ,其中
角的全等三角尺按图1方式摆放在一起 ,其中![]() .同时,要求班内各小组对图形进--步操作变换并提出问题,请你帮各小组进行解答.
.同时,要求班内各小组对图形进--步操作变换并提出问题,请你帮各小组进行解答.
[独立思考]
(1)张老师首先提出问题:图1中,四边形![]() 是平行四边形吗?说明理由;
是平行四边形吗?说明理由;
[提出问题]
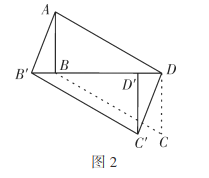
(2)如图2,“励志”小组将![]() 沿射线
沿射线![]() 方向平移到
方向平移到![]() 的位置,分别连接
的位置,分别连接![]() ,进一步提出问题:四边形
,进一步提出问题:四边形![]() 是平行四边形吗?说明理由;
是平行四边形吗?说明理由;
[拓展延伸]
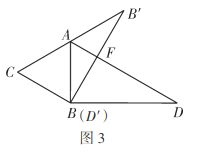
(3)“慎密”小组提出的问题是:如图3,两个全等的三角尺重叠放在![]() 的位置,将其中一个三角尺绕着点
的位置,将其中一个三角尺绕着点![]() 按逆时针方向旋转至
按逆时针方向旋转至![]() 的位置,使点
的位置,使点![]() 恰好落在边
恰好落在边![]() 上,
上,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】(1)四边形![]() 是平行四边形,理由见解析;(2)四边形
是平行四边形,理由见解析;(2)四边形![]() 是平行四边形,理由见解析;(3)
是平行四边形,理由见解析;(3)![]()
【解析】
(1)根据两组对边分别相等,即可判断四边形![]() 是平行四边形;
是平行四边形;
(2)根据一组对边平行且相等,即可判断四边形![]() 是平行四边形;
是平行四边形;
(3)根据题意可得![]() ,△ABC是等边三角形,可推出
,△ABC是等边三角形,可推出![]() ,可得
,可得![]() ,根据勾股定理即可得出
,根据勾股定理即可得出![]() 的长.
的长.
解:(1)四边形![]() 是平行四边形,
是平行四边形,
理由:∵两块三角尺全等,
∴![]() ,
,
∴四边形![]() 是平行四边形;
是平行四边形;
(2)四边形![]() 是平行四边形,
是平行四边形,
理由:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
且![]() ,
,
由平移的性质可得:![]() ,
,
且![]() ,
,
∴![]() ,
,
且![]() ,
,
∴四边形![]() 是平行四边形;
是平行四边形;
(3)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴△ABC是等边三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,根据勾股定理得
中,根据勾股定理得![]() ,
,
∴![]() 的长为
的长为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,AD为∠CAF的角平分线,BD=CD,∠DBC=∠DCB,∠DCA=∠ABD,过D作DE⊥AC于E,DF⊥AB交BA的延长线于F,则下列结论:①△CDE≌△BDF;②CE=AB+AE;③∠BDC=∠BAC;④∠DAF=∠CBD.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中的网格由单位正方形构成,![]() 中,
中,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() .
.
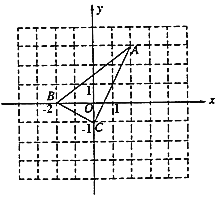
(1)![]() 的长为_______;
的长为_______;
(2)求证:![]() ;
;
(3)若以![]() 、
、![]() 、
、![]() 及点
及点![]() 为顶点的四边形为平行四边形,写出
为顶点的四边形为平行四边形,写出![]() 点在第一象限时的坐标______.
点在第一象限时的坐标______.
查看答案和解析>>
科目:初中数学 来源: 题型:
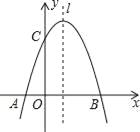
【题目】如图,已知抛物线y=![]() +mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0),
(1)求m的值及抛物线的顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在长方形ABCD中,AB=8cm,BC=12cm,E为AB的中点,动点P在线段BC上以4cm/s的速度由点B向C运动,同时,动点Q在线段CD上由点C向点D运动,设运动时间为t(s).
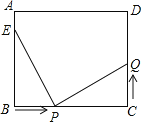
(1)当t=2时,求△EBP的面积;
(2)若动点Q以与动点P不同的速度运动,经过多少秒,△EBP与△CQP全等?此时点Q的速度是多少?
(3)若动点Q以(2)中的速度从点C出发,动点P以原来的速度从点B同时出发,都逆时针沿长方形ABCD的四边形运动,经过多少秒,点P与点Q第一次在长方形ABCD的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CD是△ABC中∠ACB的角平分线,E是AC上的一点,且CD2=BC·CE,AD=6,AE=4.
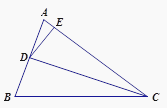
(1)求证:△BCD∽△DCE;
(2)求证:△ADE∽△ACD;
(3)求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标为A(0,3)、B(3,4)、C(2,2),(正方形网格中,每个小正方形边长为1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1;
(2)以B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比2∶1,直接写出C2点坐标是 ;
(3)△A2BC2的面积是 平方单位.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com