
����Ŀ����ͼ��ʾ���ڳ�����ABCD�У�AB=8cm��BC=12cm��EΪAB���е㣬����P���߶�BC����4cm/s���ٶ��ɵ�B��C�˶���ͬʱ������Q���߶�CD���ɵ�C���D�˶������˶�ʱ��Ϊt��s����
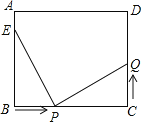
��1����t=2ʱ������EBP�������
��2��������Q���붯��P��ͬ���ٶ��˶������������룬��EBP����CQPȫ�ȣ���ʱ��Q���ٶ��Ƕ��٣�
��3��������Q�ԣ�2���е��ٶȴӵ�C����������P��ԭ�����ٶȴӵ�Bͬʱ����������ʱ���س�����ABCD���ı����˶������������룬��P���Q��һ���ڳ�����ABCD����������������
���𰸡���1��S��EBP=16cm2����2������![]() �룬��EBP����CQPȫ�ȣ���ʱ��Q���ٶ���
�룬��EBP����CQPȫ�ȣ���ʱ��Q���ٶ���![]() cm/s����3������9�룬��P���Q��һ���ڳ�����ABCD�ı�AB��������
cm/s����3������9�룬��P���Q��һ���ڳ�����ABCD�ı�AB��������
��������
��1��ֱ������ֱ�������������������ֱ�DZ߳˻���һ����㼴�ɣ�
��2����EBP���CQPȫ�ȣ�Ҫ�������������ۣ���EBP�ա�PCQ���EBP�ա�QCP�������t��ֵ�������Q���ٶȣ�
��3�����������⣬���ݵ�����ϵ����P�˶�·��=��Q�˶�·��+12���з�����⼴�ɣ�
��1����t=2ʱ��BP=2��4cm=8cm
��EΪAB���е㣬
��BE=![]() AB=
AB=![]() ��8cm=4cm��
��8cm=4cm��
�߳�����ABCD
���B=90��
��S��EBP=![]() BEBP=
BEBP=![]() ��4��8=16��cm2����
��4��8=16��cm2����
��2�����Q���ٶ���acm/s����BP=4t��cm����CQ=at��cm����
��PC=��12-4t����cm����
�ߡ�EBP����CQPȫ�ȣ���B=��C=90��
���EBP�ա�PCQ����EBP�ա�QCP
����EBP�ա�PCQʱ��PC=EB��CQ=BP
��12-4t=4�����t=2��
��2a=4��2
��a=4���붯��Q���붯��P��ͬ���ٶ��˶�ì�ܣ�
����EBP�ա�QCPʱ��CP=BP��CQ=BE
��12-4t=4t�����t=![]() ��
��
��![]() a=4�����a=
a=4�����a=![]() ��cm/s����
��cm/s����
�𣺾���![]() �룬��EBP����CQPȫ�ȣ���ʱ��Q���ٶ���
�룬��EBP����CQPȫ�ȣ���ʱ��Q���ٶ���![]() cm/s��
cm/s��
��3���辭��x�룬��P���Q��һ���ڳ�����ABCD�ı���������
��4x=12+![]() x����ã�x=9
x����ã�x=9
��ʱ��P�˶�·��Ϊ��4��9=36��cm�������P��AB���е㴦��
�𣺾���9�룬��P���Q��һ���ڳ�����ABCD�ı�AB��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
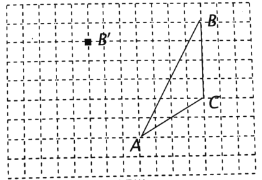
����Ŀ����ͼ���ڷ���ֽ�ڽ�![]() ����һ��ƽ�ƺ�õ�
����һ��ƽ�ƺ�õ�![]() ��ͼ�б���˵�
��ͼ�б���˵�![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() .��С�����α߳�Ϊ1��
.��С�����α߳�Ϊ1��![]() �Ķ����ΪС�����εĶ��㣩
�Ķ����ΪС�����εĶ��㣩
��1����ȫ![]() ��
��
��2������![]() ��
��![]() ���ϵ�����
���ϵ�����![]() ��
��
��3������![]() ��
��![]() ���ϵĸ���
���ϵĸ���![]() ��
��
��4��![]() �����Ϊ_____.
�����Ϊ_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
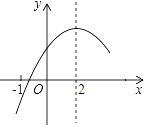
����Ŀ�����κ���y=ax2+bx+c��a��0���IJ���ͼ����ͼ����ʾ��ͼ����㣨��1��0�����Գ���Ϊֱ��x=2������ �н�������ȷ�ĸ����У� ��
��4a+b=0��
��9a+3b+c��0��
������A����3��y1������B����![]() ��y2������C��5��y3���ڸú���ͼ���ϣ���y1��y3��y2��
��y2������C��5��y3���ڸú���ͼ���ϣ���y1��y3��y2��
��������a��x+1����x��5��=��3������Ϊx1��x2 �� ��x1��x2 �� ��x1����1��5��x2 ��
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����²��ϣ�����Ҫ�������Ӧ������
����ѧϰ:��ν�һԪ���β���ʽ��
����:��һԪ���β���ʽ![]() ��
��
�⣺![]()
![]() ��
��
���������ij˷�������������ˣ�ͬ�ŵ��������У�
![]()
![]()
�ⲻ��ʽ��![]() ��:
��:![]()
�ⲻ��ʽ��![]() ��:
��:![]()
![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ��
��![]() ��
��
��:һԪ���β���ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ��
��![]() ��
��
����1�������һԪ���β���ʽ�Ĺ��������ֳ�����ѧ��һЩ����˼�뷽������������ѡ����ѡ������Ϊ��ȷ��һ�_____ ��(��ѡ���)
A.��������˼�룻B.���ν��˼�룻C.������˼�룻D.����˼��
��2����һԪ���β���ʽ![]() �Ľ⼯Ϊ��_____ ��(ֱ����д�������д������)
�Ľ⼯Ϊ��_____ ��(ֱ����д�������д������)
��3�����������е���ѧ˼�뷽�������ʽ����ʽ![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
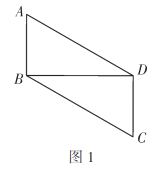
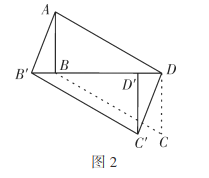
ͼ�α任�Ļ�����ʽ��:ƽ�Ʊ任����ת�任����ԳƱ任.����ѧ�ۺ���ʵ�����ϣ�����ʦ�����麬![]() �ǵ�ȫ�����dz߰�ͼ1��ʽ�ڷ���һ�� ������
�ǵ�ȫ�����dz߰�ͼ1��ʽ�ڷ���һ�� ������![]() .ͬʱ��Ҫ����ڸ�С���ͼ�ν�--�������任��������⣬������С����н��.
.ͬʱ��Ҫ����ڸ�С���ͼ�ν�--�������任��������⣬������С����н��.
[����˼��]
��1������ʦ�����������:ͼ1�У��ı���![]() ��ƽ���ı�����˵�����ɣ�
��ƽ���ı�����˵�����ɣ�
[�������]
��2����ͼ2������־��С�齫![]() ������
������![]() ����ƽ�Ƶ�
����ƽ�Ƶ�![]() ��λ�ã��ֱ�����
��λ�ã��ֱ�����![]() ����һ��������⣺�ı���
����һ��������⣺�ı���![]() ��ƽ���ı�����˵�����ɣ�
��ƽ���ı�����˵�����ɣ�
[��չ����]
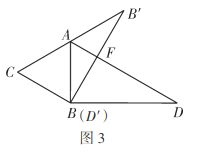
��3�������ܡ�С������������ǣ���ͼ3������ȫ�ȵ����dz��ص�����![]() ��λ�ã�������һ�����dz����ŵ�
��λ�ã�������һ�����dz����ŵ�![]() ����ʱ�뷽����ת��
����ʱ�뷽����ת��![]() ��λ�ã�ʹ��
��λ�ã�ʹ��![]() ǡ�����ڱ�
ǡ�����ڱ�![]() �ϣ�
�ϣ�![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
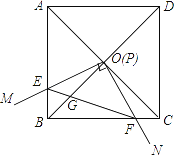
����Ŀ����ͼ���߳�Ϊ1��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����ֱ����MPN��ʹֱ�Ƕ���P���O�غϣ�ֱ�DZ�PM��PN�ֱ���OA��OB�غϣ�Ȼ����ʱ����ת��MPN����ת��Ϊ�ȣ�0�㣼�ȣ�90�㣩��PM��PN�ֱ�AB��BC��E��F���㣬����EF��OB�ڵ�G�������н�������ȷ����________��
��1��EF=![]() OE����2��S�ı���OEBF��S������ABCD=1��4����3��BE+BF=
OE����2��S�ı���OEBF��S������ABCD=1��4����3��BE+BF= ![]() OA����4������ת�����У�����BEF����COF�����֮�����ʱ��AE=
OA����4������ת�����У�����BEF����COF�����֮�����ʱ��AE=![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ֻ�Խ��Խ�ܵ����ڵ�ϲ�������ֿ�ʽ���Ͷ���г���ij�꾭Ӫ��A���ֻ�ȥ�������ܶ�Ϊ50000Ԫ������ÿ�����ۼ۱�ȥ�꽵��400Ԫ����������������ͬ�������ܶ��ȥ�����![]() ��
��
A��B�����ֻ��Ľ��������ۼ۸����±���
A���ֻ� | B���ֻ� | |
�����۸� | 1100 | 1400 |
���ۼ۸� | ��������ۼ۸� | 2000 |
��1������A���ֻ�ÿ���ۼ۶���Ԫ��
��2���õ�ƻ��½�һ��A���ֻ���B���ֻ���60������B���ֻ��Ľ�������������A���ֻ�������������Ӧ��ν�������ʹ�����ֻ�������ࣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڽ���ƽ��ֱ������ϵ������ֽ�У�ÿ��С�����DZ߳�Ϊ1����λ���ȵ�С�����Σ���ABC�Ķ�����ڸ���ϣ���P������Ϊ��-1��0����
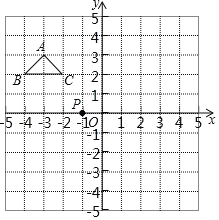
��1������ABC�Ƶ�P��ת180���õ���A��B��C����������A��B��C����
��2������ABC����ƽ��7����λ���ȵõ���A��B��C�壬������A��B��C�壻
��3����A��B��C�����A��B��C���Ƿ�����ĶԳƣ����ǣ����ҳ��Գ�����P������д�������ꣻ�����ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C��90����ADƽ����CAB��DE��AB��E����AC��6��BC��8��
��1����DE�ij���
��2������ADB�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com