
【题目】若多项式![]() 的次数为
的次数为![]() ,项数为
,项数为![]() ;当
;当![]() 时,此多项式的值为
时,此多项式的值为![]() .
.
(1)分别写出![]() 所表示的数,并计算代数式
所表示的数,并计算代数式![]() 的值;
的值;
(2)设有理数0,![]() ,
,![]() ,
,![]() 在数轴上对应的点分别是点
在数轴上对应的点分别是点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() .
.
①请比较线段![]() 与线段
与线段![]() 的大小.
的大小.
②若点![]() 是线段
是线段![]() 上的一动点,比较
上的一动点,比较![]() 与
与![]() 的大小,说明理由.
的大小,说明理由.
【答案】(1)a=2,b=3,c=-7,![]() =14;(2)①OB<AC;②
=14;(2)①OB<AC;②![]() ≤PB.
≤PB.
【解析】
(1)根据多项式的系数及项数的定义可得a、b的值,把m=-1代入多项式可得c的值,把a、b、c的值代入所求代数式即可得答案;
(2)①根据a、b、c的值,利用数轴上两点间的距离公式可求出OB、AC的长,比较即可得答案;
②根据PA+PC=AC可求出![]() 的值,根据a、b的值可求出AB的值,根据PB=AB+PA即可比较
的值,根据a、b的值可求出AB的值,根据PB=AB+PA即可比较![]() 与PB的大小.
与PB的大小.
(1)∵多项式![]() 中,次数最高的项的次数为2,共有3项,
中,次数最高的项的次数为2,共有3项,
∴a=2,b=3,
∵m=-1时,![]() 的值为c,
的值为c,
∴c=1-5-3=-7,
∴![]() =49-21-14=14.
=49-21-14=14.
(2)①∵a=2,b=3,c=-7,
∴OB=![]() =3,AC=
=3,AC=![]() =9,
=9,
∴OB<AC.
②∵点![]() 是线段
是线段![]() 上的一动点,
上的一动点,
∴PA+PC=AC=9,
∴![]() =1,
=1,
∵a=2,b=3,
∴AB=![]() =1,
=1,
∵PB=PA+AB,PA≥0(点P与点A重合时PA=0),
∴PB≥1,
∴![]() ≤PB.
≤PB.


科目:初中数学 来源: 题型:
【题目】如图四边形ABCD是正方形,点E、F分别在线段BC、DC上,∠BAE=30°.若线段AE绕点A逆时针旋转后与线段AF重合,则旋转的角度是( )

A.30°B.45°C.60°D.90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2013的直角顶点的坐标为______________.
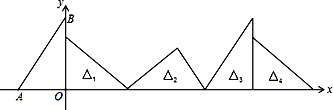
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,点A、B的横坐标分别为a、a+2,二次函数![]() 的图象经过点A、B,且a、m满足2a﹣m=d(d为常数).
的图象经过点A、B,且a、m满足2a﹣m=d(d为常数).
(1)若一次函数y1=kx+b的图象经过A、B两点.
①当a=1、d=﹣1时,求k的值;
②若y1随x的增大而减小,求d的取值范围;
(2)当d=﹣4且a≠﹣2、a≠﹣4时,判断直线AB与x轴的位置关系,并说明理由;
(3)点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形,将一块含有30°角的直角三角尺DEF按如图所示放置,让三角尺在BC所在的直线上向右平移.如图①,当点E与点B重合时,点A恰好落在三角尺的斜边DF上.
(1)利用图①证明:EF=2BC.
(2)在三角尺的平移过程中,在图②中线段AH=BE是否始终成立(假定AB,AC与三角尺的斜边的交点分别为G,H)?如果成立,请证明;如果不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,且
,且![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,
![]()
(1)![]() _____________,
_____________,![]() _________________;
_________________;
(2)若将数轴折叠,使得![]() 点与
点与![]() 点重合,则点
点重合,则点![]() 与数 表示的点重合.
与数 表示的点重合.
(3)在(1)(2)的条件下,若点![]() 为数轴上一动点,其对应的数为
为数轴上一动点,其对应的数为![]() ,当代数式
,当代数式![]() 取得最小值时,此时
取得最小值时,此时![]() ____________,最小值为__________________.
____________,最小值为__________________.
(4)在(1)(2)的条件下,若在点![]() 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点![]() 处以
处以![]() 个单位
个单位![]() 秒的速度向左运动;同时另一小球乙从点
秒的速度向左运动;同时另一小球乙从点![]() 处以
处以![]() 个单位
个单位![]() 秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)以原来的速度向相反的方向运动,设运动的时间为
秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看做一点)以原来的速度向相反的方向运动,设运动的时间为![]() (秒),请表示出甲、乙两小球之间的距离
(秒),请表示出甲、乙两小球之间的距离![]() (用
(用![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com