
 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中成立的有①②③.(只填序号)
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中成立的有①②③.(只填序号)分析 先证明∠DFC=∠BCF,再证明DF=CD,得出∠DFC=∠DCF,即可得出①正确;
连接CF并延长交BA的延长线于G,先证明CF=GF,再由直角三角形斜边上的中线性质得出②正确;
由EF=GF得出∠G=∠FEG,再证明AF=AG,得出∠G=∠AFG=∠DFC,即可得出③正确.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠DFC=∠BCF,
∵AD=2AB,F是AD的中点,
∴DF=CD,
∴∠DFC=∠DCF,
∴∠BCF=∠DCF,
∴∠DCF=$\frac{1}{2}$∠BCD,
∴①正确;
连接CF并延长交BA的延长线于G,如图所示: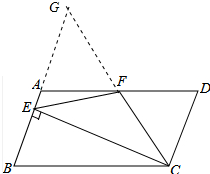 ∵F是AD的中点,AB∥CD,
∵F是AD的中点,AB∥CD,
∴CF=GF,
∵CE⊥AB,
∴∠CEG=90°,
∴EF=$\frac{1}{2}$CG=CF=GF,
∴②正确;
∵EF=GF,
∴∠G=∠FEG,
∵AD∥BC,CF=GF,
∴AG=AB,
∴AF=AG,
∴∠G=∠AFG=∠DFC,
∵∠CFE=∠G+∠AEF,
∴∠DFE=∠CFE+∠DFC=3∠AEF,
∴③正确;
故答案为:①②③.
点评 本题考查了平行四边形的性质、直角三角形斜边上的中线性质、等腰三角形的判定与性质;熟练掌握平行四边形的性质,并能进行有关推理论证是解决问题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:选择题
| A. | =$\frac{2}{3}$ | B. | >$\frac{2}{3}$ | C. | ≤$\frac{2}{3}$ | D. | ≥$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=$\sqrt{2}$,CE=3$\sqrt{2}$,H是AF的中点,那么CH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=$\sqrt{2}$,CE=3$\sqrt{2}$,H是AF的中点,那么CH的长是( )| A. | 3.5 | B. | $\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
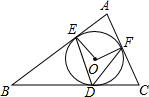 如图,⊙O内切于△ABC,切点分别为D,E,F,连接OE,OF,DE,DF,乙组∠A=80°,则∠EDF等于( )
如图,⊙O内切于△ABC,切点分别为D,E,F,连接OE,OF,DE,DF,乙组∠A=80°,则∠EDF等于( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
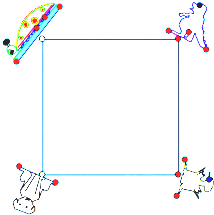 如图,4个小动物分别站在正方形场地的4个顶点,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?
如图,4个小动物分别站在正方形场地的4个顶点,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动,当它们同时停止时,顺次连接4个动物所在地点围成的图形是什么形状?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com