【题目】如图，在⊙O中，半径OA＝6 cm，C是OB的中点，∠AOB＝120°，求阴影部分的面积．
【答案】阴影部分的面积为
cm2.
【解析】
过点C作CD⊥AO，交AO的延长线于点D，在Rt△OCD中，求得CD 的长，即可求得△AOC的面积，再求得扇形AOB的面积，利用S阴影＝S扇形OAB－S△AOC即可求得阴影部分的面积.
过点C作CD⊥AO，交AO的延长线于点D，
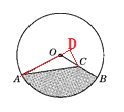
∵OB＝6 cm，C为OB的中点，∴OC＝3 cm.
∵∠AOB＝120°，∴∠COD＝60°.∴∠OCD＝30°.
∴在Rt△CDO中，OD＝
OC＝
cm.
∴CD＝
＝
＝
(cm)．
∴S△AOC＝AO·CD＝×6×＝
(cm2)．
又∵S扇形OAB＝
＝12π(cm2)，
∴S阴影＝S扇形OAB－S△AOC＝12π－＝
(cm2)，
即阴影部分的面积为cm2.
习题精选系列答案科目：初中数学 来源： 题型：
【题目】《如果想毁掉一个孩子，就给他一部手机!》这是2017年微信圈一篇热传的文章．国际上，法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机．为了解学生手机使用情况，某学校开展了“手机伴我健康行”主题活动，他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，②的 统计图，已知“查资料”的人数是 40人．请你根据以上信息解答下列问题：
(1)在扇形统计图中，“玩游戏”对应的百分比为______，圆心角度数是______度；
(2)补全条形统计图；
(3)该校共有学生2100人，估计每周使用手机时间在2 小时以上(不含2小时)的人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
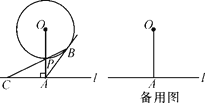
【题目】如图，已知直线l与⊙O相离，OA⊥l于点A，OA＝5，OA与⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系，并说明理由；
(2)若在⊙O上存在点Q，使△QAC是以AC为底边的等腰三角形，求⊙O的半径r的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商家计划从厂家采购空调和冰箱两种产品共20台，空调的采购单价y1（元/台）与采购数量x1（台）满足y1=﹣20x1+1500（0＜x1≤20，x1为整数）；冰箱的采购单价y2（元/台）与采购数量x2（台）满足y2=﹣10x2+1300（0＜x2≤20，x2为整数）．
（1）经商家与厂家协商，采购空调的数量不少于冰箱数量的
，且空调采购单价不低于1200元，问该商家共有几种进货方案？
（2）该商家分别以1760元/台和1700元/台的销售单价售出空调和冰箱，且全部售完．在（1）的条件下，问采购空调多少台时总利润最大？并求最大利润．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某超市开展早市促销活动，为早到的顾客准备一份简易早餐，餐品为四样A：菜包、B：面包、C：鸡蛋、D：油条．超市约定：随机发放，早餐一人一份，一份两样，一样一个．
（1）按约定，“某顾客在该天早餐得到两个鸡蛋”是 事件（填“随机”、“必然”或“不可能”）；
（2）请用列表或画树状图的方法，求出某顾客该天早餐刚好得到菜包和油条的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在□ABCD，过点D作DE⊥AB于点E，点F在边CD上，DF＝BE，连接AF，BF.
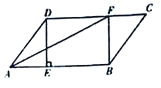
（1）求证：四边形BFDE是矩形；
（2）若CF＝3，BF＝4，DF＝5，求证：AF平分∠DAB.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，BC是路边坡角为30°，长为10米的一道斜坡，在坡顶灯杆CD的顶端D处有一探射灯，射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°（图中的点A、B、C、D、M、N均在同一平面内，CM∥AN）．
（1）求灯杆CD的高度；
（2）求AB的长度（结果精确到0.1米）．（参考数据：
=1.73．sin37°≈060，cos37°≈0.80，tan37°≈0.75）
查看答案和解析>>
科目：初中数学 来源： 题型：
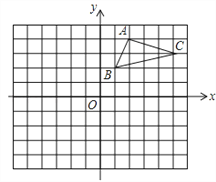
【题目】如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4）.
（1）画出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标A1 ________________．
（2）画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2，并写出点A2的坐标A2__________________．
(3) △ABC是否为直角三角形？答_________（填是或者不是）.
（4）利用格点图，画出BC边上的高AD，并求出AD的长，AD=_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
