
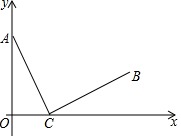
 已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC.
已知,点C(4,0)在x轴上,动点A(0,m)在y轴上,线段CB出线段CA绕点C顺时针旋转90°得到,如图所示,∠ACB=90°,AC=BC.分析 (1)先过点B作BD⊥x轴于点D,根据AAS判定△ACO≌△CBD,根据全等三角形的对应边相等,得出BD=4,OD=10,求得点B的坐标;
(2)先过点B作BD⊥x轴于点D,根据AAS判定△ACO≌△CBD,根据全等三角形的对应边相等,得出BD=4,OD=2,求得点B的坐标;
(3)过点B作BD⊥x轴于点D,根据全等三角形的性质,求得BD=CO=4,再根据垂线段最短,得出当点D与点Q重合时,BQ最小,求得此时AO=CQ=5,即可得到m的值.
解答 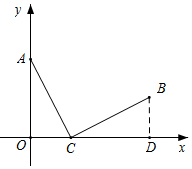 解:(1)如图所示,当m=6时,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,
解:(1)如图所示,当m=6时,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,
∵∠ACB=90°,AC=BC,
∴∠CAO+∠ACO=∠BCD+∠ACO=90°,
∴∠CAO=∠BCD,
∴△ACO≌△CBD(AAS),
∵C(4,0),A(0,6),
∴BD=CO=4,CD=AO=6,
∴OD=10,
∴此时,点B的坐标为(10,4);
(2)如图所示,当m=6时,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,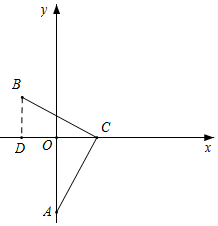
∵∠ACB=90°,AC=BC,
∴∠CAO+∠ACO=∠BCD+∠ACO=90°,
∴∠CAO=∠BCD,
∴△ACO≌△CBD(AAS),
∵C(4,0),A(0,-6),
∴BD=CO=4,CD=AO=6,
∴OD=2,
∴此时,点B的坐标为(-2,4);
(3)如图所示,过点B作BD⊥x轴于点D,则∠CDB=∠AOC=90°,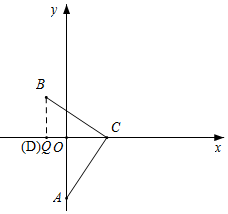
∵∠ACB=90°,AC=BC,
∴∠CAO+∠ACO=∠BCD+∠ACO=90°,
∴∠CAO=∠BCD,
∴△ACO≌△CBD(AAS),
∵C(4,0),
∴BD=CO=4,
连接BQ,则当点D与点Q重合时,BD=BQ=4,
根据垂线段最短,可知此时BQ最小,
∵Q(-1,0),C(4,0),
∴此时,AO=CQ=5,
又∵点A在y轴负半轴上,
∴m的值为-5.
点评 本题主要考查了全等三角形的判定与性质,垂线段最短的综合应用,解决问题的关键是作辅助线构造全等三角形,运用全等三角形的对应边相等进行计算求解.实际问题中涉及线路最短问题时,其理论依据应从“两点之间,线段最短”和“垂线段最短”这两个中去选择.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源:2017届江苏省扬州市九年级下学期第一次月考数学试卷(解析版) 题型:解答题
在一个不透明的盒子中,放入2个白球和1个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出2个球,请通过列表或树状图求摸出2个球都是白球的概率;
(2)搅匀后从中任意摸出1个球,记录下颜色后放回袋中,再次搅匀后从中任意摸出1个球,请通过列表或树状图求2次摸出的球都是白球的概率;
(3)现有一个可以自由转动的转盘,转盘被等分成60个相等的扇形,这些扇形除颜色外完全相同,其中40个扇形涂上白色,20个扇形涂上红色,转动转盘2次,指针2次都指向白色区域的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
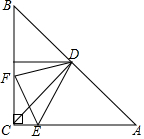 已知△ACB为等腰直角三角形,D为BA的中点,∠EDF=45°,交AC于E点,交BC于F点,连EF.
已知△ACB为等腰直角三角形,D为BA的中点,∠EDF=45°,交AC于E点,交BC于F点,连EF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1,有以下四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴是x=1,有以下四个结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com