
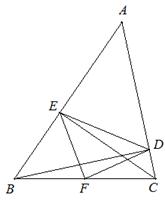
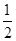 BC=DF;故△DEF为等腰三角形;
BC=DF;故△DEF为等腰三角形;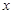 ,则∠DFE=2
,则∠DFE=2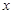 ,用(2)类似的方法求出∠DFE=30°,作出△EDF边DF上的高EG,求出EG的长即可.
,用(2)类似的方法求出∠DFE=30°,作出△EDF边DF上的高EG,求出EG的长即可.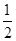 BC=DF,∴△DEF是等腰三角形.
BC=DF,∴△DEF是等腰三角形.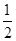 BC=DF,∴∠EBF=∠FEB,同理,∠DCF=∠FDC,∴∠FEB+∠FDC=135°,
BC=DF,∴∠EBF=∠FEB,同理,∠DCF=∠FDC,∴∠FEB+∠FDC=135°,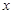 ,∠DFE=2
,∠DFE=2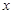 ,∵EF=BF,DF=FC,∴∠FBE=∠BEF,∠FCD=∠FDC,
,∵EF=BF,DF=FC,∴∠FBE=∠BEF,∠FCD=∠FDC, ,∵
,∵
 ,∴∠DFE=2
,∴∠DFE=2 ,∵BC=4,∴DF=EF=2,∴EG=1,∴△DEF面积1.
,∵BC=4,∴DF=EF=2,∴EG=1,∴△DEF面积1.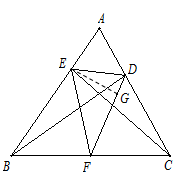


科目:初中数学 来源:不详 题型:解答题
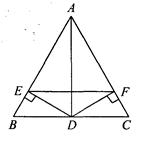
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
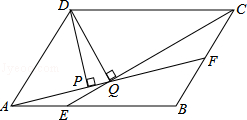
| A.3:4 | B.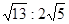 | C.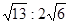 | D.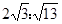 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.具备①②④ | B.具备①②⑤ | C.具备①⑤⑥ | D.具备①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com