
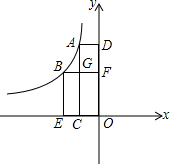
 如图,点A,B是双曲线y=$\frac{k}{x}$上的点,分别经过A,B两点向x轴,y轴作垂线,垂足分别为点C,D,E,F,AC与BF交于点G,若S四边形OCGF=2,S四边形AGFD+S四边形BECG=6,则k=-5.
如图,点A,B是双曲线y=$\frac{k}{x}$上的点,分别经过A,B两点向x轴,y轴作垂线,垂足分别为点C,D,E,F,AC与BF交于点G,若S四边形OCGF=2,S四边形AGFD+S四边形BECG=6,则k=-5.  名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
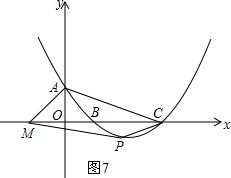
 如图,抛物线y=-$\frac{1}{2}$x2+4x-6与x轴相交于点A,B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.
如图,抛物线y=-$\frac{1}{2}$x2+4x-6与x轴相交于点A,B,与y轴相交于点C,抛物线的对称轴与x轴相交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
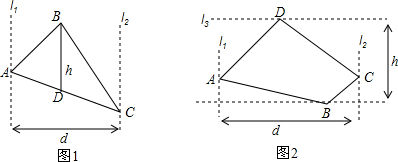
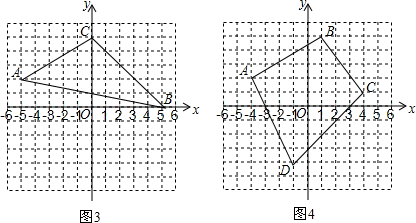
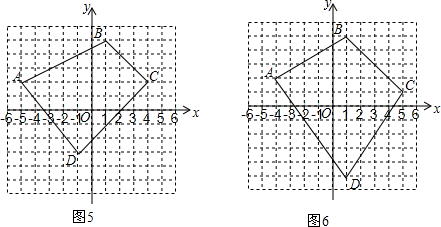
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
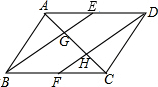 如图,?ABCD中,E,F分别是边AD,BC中点,AC分别交BE,DF于点G,H,请判断下列结论中正确的有( )
如图,?ABCD中,E,F分别是边AD,BC中点,AC分别交BE,DF于点G,H,请判断下列结论中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
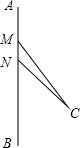 “村村通公路”工程是国家为支持新农村建设的一项重大举措,为了落实这一举措,重庆潼南县政府计划在南北方向的A、B两村之间建一条公路AB.已知公路AB的一侧有C村,在公路AB上的M处测得C村在M的南偏东37°方向上,从M向南走270米到达N处,测得C村在N的东南方向上,且C村周围800米范围内为油菜花田,那么计划修建的公路AB是否会穿过油菜花田,请说明理由(参考数据:sin37°≈0.8,cos37°≈0.8,tan37°≈0.75)
“村村通公路”工程是国家为支持新农村建设的一项重大举措,为了落实这一举措,重庆潼南县政府计划在南北方向的A、B两村之间建一条公路AB.已知公路AB的一侧有C村,在公路AB上的M处测得C村在M的南偏东37°方向上,从M向南走270米到达N处,测得C村在N的东南方向上,且C村周围800米范围内为油菜花田,那么计划修建的公路AB是否会穿过油菜花田,请说明理由(参考数据:sin37°≈0.8,cos37°≈0.8,tan37°≈0.75)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com