
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
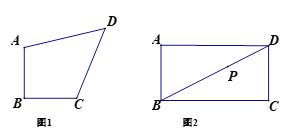
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,则对角线BD的长为 ;
②若AC⊥BD,求证:AD=CD;
(2)如图2,在矩形ABCD中,AB=5,BC=9,点![]() 是对角线
是对角线![]() 上一点,且
上一点,且![]() ,过点
,过点![]() 作直线分别交边
作直线分别交边![]() 于点
于点![]() ,使四边形
,使四边形![]() 是等腰直角四边形.直接写出
是等腰直角四边形.直接写出![]() 的长为 .
的长为 .
【答案】(1)①![]() ;②见解析;(2)5或6.5.
;②见解析;(2)5或6.5.
【解析】
(1)①根据有一组对边平行且相等的四边形是平行四边形可证得四边形ABCD是平行四边形;根据邻边相等的平行四边形是菱形可证得四边形ABCD是菱形;根据有一个角是直角的菱形是正方形可证得四边形ABCD是正方形,从而求出对角边即可.
②根据全等三角形的判定定理可得出三角形全等,然后得出对应边相等即可.
(2)紧抓等腰直角四边形的概念,分类讨论,先根据图形定义可直接得出AE的长度,再结合相似三角形的性质和判定定理可求出AE的长度.
解:(1)①∵AB=CD,AB∥CD,
∴四边形ABCD是平行四边形,
又AB=BC,∠ABC=90°,
∴四边形ABCD是正方形,
∴BD=AC=![]() =
=![]()
所以答案为![]() .
.
②如图1,连接AC,BD,
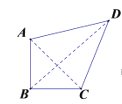
∵AB=BC,AC⊥BD,
∴∠ABD=∠CBD,
又∵BD=BD,
∴△ABD≌△CBD,
∴AD=CD.
(2)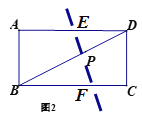
因为四边形ABFE是等腰直角四边形,
所以可以是AB=AE或AB=BF.
当AB=AE时,AE=AB=5,
当AB=BF时,BF=5
∵DE∥BF,
∴△DPE∽△BPF,
∴![]() ,
,
∴DE=2.5
∴AE=9-2.5=6.5
综上,AE结果为5或6.5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从相距420km的A、B两地相向而行,乙车比甲车先出发1小时,两车分别以各自的速度匀速行驶,途经C地(A、B、C三地在同一条直线上).甲车到达C地后因有事立即按原路原速返回A地,乙车从B地直达A地,甲、乙两车距各自出发地的路程y(千米)与甲车行驶所用的时间x(小时)的关系如图所示,结合图象信息回答下列问题:
(1)甲车的速度是 千米/时,乙车的速度是 千米/时;
(2)求甲车距它出发地的路程y(千米)与它行驶所用的时间x(小时)之间的函数关系式;
(3)甲车出发多长时间后两车相距90千米?请你直接写出答案.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品店购进A,B两种工艺品,已知这两种工艺品的单价之和为200元,购进2个A种工艺品和3个B种工艺品需花费520元.
(1)求A,B两种工艺品的单价;
(2)该店主欲用9600元用于进货,且最多购进A种工艺品36个,B种工艺品的数量不超过A种工艺品的2倍,则共有几种进货方案?
(3)已知售出一个A种工艺品可获利10元,售出一个B种工艺品可获利18元,该店主决定每售出一个B种工艺品,为希望工程捐款m元,在(2)的条件下,若A,B两种工艺品全部售出后所有方案获利均相同,则m的值是多少?此时店主可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十三五”以来,党中央,国务院不断加大脱贫攻坚的支持决策力度,并出台配套文件,国家机关各部门也出台多项政策文件或实施方案.某单位认真分析被帮扶人各种情况后,建议被帮扶人大力推进特色产业,大量栽种甜橙;同时搭建电商运营服务平台,开设网店销售农产品橙.丰收后,将一批甜橙采取现场销售和网络销售相结合进行试销,统计后发现:同样多的甜橙,现场销售可获利800元,网络销售则可获利1000元,网络销售比现场销售每件多获利5元
(1)现场销售和网络销售每件分别多少元?
(2)根据甜橙试销情况分析,现场销售量a(件)和网络销售量b(件)满足如下关系式:b=﹣![]() a2+12a﹣200.求a为何值时,农户销售甜橙获得的总利润最大?最大利润是多少?
a2+12a﹣200.求a为何值时,农户销售甜橙获得的总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最小值是_____.
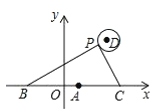
查看答案和解析>>
科目:初中数学 来源: 题型:
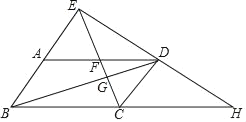
【题目】如图,四边形ABCD是平行四边形,连接BD,点E在BA的延长线上,连接EC,分别交AD、BD于点F、点G,连接ED并延长交BC的延长线于点H,则下列结论错误的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
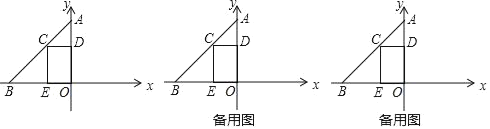
【题目】如图,在平面直角坐标系中,点O为坐标原点,点A在y轴的正半轴上,点B在x轴的负半轴上,点C是线段AB上一动点CD⊥y轴于点D,CE⊥x轴于点E,OA=6,AD=OE.
(1)求直线AB的解析式;
(2)连接ED,过点C作CF⊥ED,垂足为F,过点B作x轴的垂线交FC的延长线于点G,求点G的坐标;
(3)在(2)的条件下,连接AG,作四边形AOBG关于y轴的对称图形四边形AONM,连接DN,将线段DN绕点N逆时针旋转90°得到线段PN,H为OD中点,连接MH、PH,四边形MHPN的面积为40,连接FH,求线段FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
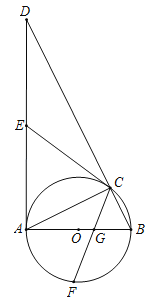
【题目】如图,![]() 为
为![]() 的内接三角形,
的内接三角形,![]() 为
为![]() 的直径,过点
的直径,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)若点![]() 为直径
为直径![]() 下方半圆的中点,连接
下方半圆的中点,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com