
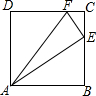
 已知正方形ABCD中,AB=5,E是BC上的一点,连接AE,过点E作EF⊥AE,交CD于点F.当E点在BC边上运动时,设线段BE的长为x,线段CF的长为y.
已知正方形ABCD中,AB=5,E是BC上的一点,连接AE,过点E作EF⊥AE,交CD于点F.当E点在BC边上运动时,设线段BE的长为x,线段CF的长为y.分析 (Ⅰ)由题意易得△CEF∽△BAE,根据对应边成比例,可得y关于x的函数解析式,根据BC的长确定定义域即可;
(Ⅱ)用配方法求得二次函数的最值即可.
解答 解:(Ⅰ)∵四边形ABCD是正方形,
∴∠B=90°,
∵EF⊥AE,
∴∠AEF=90°.
又∵∠CEA=∠CEF+∠AEF,∠CEA=∠BAE+∠B,
∴∠CEF=∠BAE,
又∵∠B=∠C=90°,
∴△CEF∽△BAE,
∴$\frac{CF}{BE}$=$\frac{CE}{AB}$,
∴$\frac{y}{x}$=$\frac{5-x}{x}$,
∴y=-$\frac{1}{5}$x2+x(0<x<5);
(Ⅱ)y=-$\frac{1}{5}$x2+x=-$\frac{1}{5}$(x-$\frac{5}{2}$)2$+\frac{5}{4}$
根据函数图象可知,抛物线y=-$\frac{1}{5}$x2+x=-$\frac{1}{5}$(x-$\frac{5}{2}$)2$+\frac{5}{4}$,
开口向下,抛物线的顶点坐标是它的最高点、且x=$\frac{5}{2}$在函数的定义域内.
所以当BE的长为$\frac{5}{2}$时,CF的长最大为$\frac{5}{4}$.
点评 此题考查了相似三角形的判定及性质的应用、二次函数的最值求法、直角三角形中锐角函数值的求法等知识点.


科目:初中数学 来源: 题型:选择题
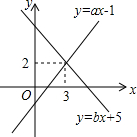 一次函数y=ax-1和y=bx+5的图象如图所示,则a、b的值是( )
一次函数y=ax-1和y=bx+5的图象如图所示,则a、b的值是( )| A. | a=3,b=2 | B. | a=2,b=3 | C. | a=1,b=-1 | D. | a=-1,b=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
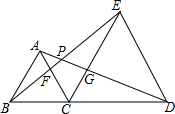 如图,△ABC和△ECD都是等边三角形,连接BE和AD,AC交BE于点F,AD交CE于点G,AD交BE于点P.
如图,△ABC和△ECD都是等边三角形,连接BE和AD,AC交BE于点F,AD交CE于点G,AD交BE于点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8% | B. | 18% | C. | 20% | D. | 25% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
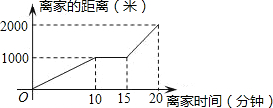 某天小明骑自行车上学,途中因发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是( )
某天小明骑自行车上学,途中因发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是( )| A. | 学校离家的距离为1000米 | |
| B. | 修车时间为5分钟 | |
| C. | 到达学校时共用时间20分钟 | |
| D. | 修车后小明骑车的速度是修车前速度的2倍 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com