练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．不等式2x+9≥4（x+1）的正整数解是1、2．

    分析 首先利用不等式的基本性质解不等式，再从不等式的解集中找出适合条件的正整数即可．

    解答 解：不等式的解集是x≤$\frac{5}{2}$，
    故不等式2x+9≥4（x+1）的正整数解为1，2．
    故答案为：1、2．

    点评 本题考查了一元一次不等式的整数解，正确解不等式，求出解集是解答本题的关键．解不等式应根据不等式的基本性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    15．计算：y（2x+y）-（x+y）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．阅读理解：已知∠A、∠B是Rt△ABC的两个锐角，锐角∠A的邻边与对边的比值叫做锐角∠A的余切，记作cotA，记cotA=$\frac{∠A的邻边}{∠A的对边}$，已知tanB=$\frac{4}{3}$，则cotB的值等于$\frac{3}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．先化简，再求值：$\frac{{x}^{2}-4x+4}{{x}^{2}-4}$÷$\frac{x-2}{{x}^{2}+2x}$+3，在0、±1、±2五个数中选择一个恰当的数x代入求值．（所选的x要使分式有意义）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．不等式x-1≤1的解集在数轴上表示正确的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．如图，△ABC是以BC为底边的等腰三角形，点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点，点B在二次函数y=$\frac{1}{8}$x2+bx+c的图象上，且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形．
    （1）试求点B、D的坐标，并求出该二次函数的解析式；
    （2）P、Q分别是线段AD、CA上的动点，点P从A开始向D运动，同时点Q从C开始向A运动，它们运动的速度都是每秒1个单位，求：
    ①当P运动到何处时，△APQ是直角三角形？
    ②当P运动到何处时，四边形PDCQ的面积最小？此时四边形PDCQ的面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，三角形ABC是直角三角形，BO是它斜边AC上的中线，延长BO至D，使OD=OB，连接AD，DC，求证：四边形ABCD是矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

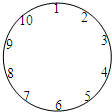    14．10个人围成一个圆圈做游戏，游戏的规则是：每人心里想好一个数，并把自己想好的数如实地告诉与他相邻的两个人，然后每人将与他相邻两个人的数据的平均数报出来，报出来的数如图所示，则报1的人心里想的数是6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

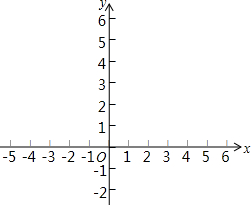    15．如图，直线AB经过点A（-3，0），B（0，2），经过点D（0，4）并且与y轴垂直的直线CD与直线AB交于第一象限内点C．
    （1）求直线AB的表达式；
    （2）在x轴上有一点Q，若△AQC的面积为8，求点Q的坐标；
    （3）在x轴的正半轴上是否存在一点P，使得△OCP为等腰三角形？若存在求出点P的坐标；若不存在，请说明理由；
    （4）在线段CA上有一动点E，联接OE，以OE为一边作正方形OEMN，请直接写出正方形OEMN的最小面积值是多少？

    查看答案和解析>>

    同步练习册答案