
 如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.分析 (1)首先得出B,D点坐标,再利用待定系数法求出二次函数解析式即可;
(2)①分别利用当PQ⊥AC时,当QP⊥AD时,结合勾股定理求出t的值即可;
②过点Q作QH⊥AD,垂足为H.由于S△APQ=$\frac{1}{2}$AP•QH=$\frac{1}{2}$AP•AQsin∠PAQ,S△ACD=$\frac{1}{2}$AD•OA,所以S四边形PDCQ=S△ACD-S△APQ求出最值即可.
解答 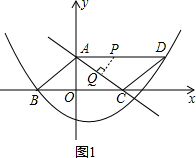 解:(1)由y=-$\frac{3}{4}$x+3,得A (0,3),C (4,0).
解:(1)由y=-$\frac{3}{4}$x+3,得A (0,3),C (4,0).
由于B、C关于OA对称,所以B(-4,0),
BC=8.
因为AD∥BC,AD=BC,所以D(8,3).
将B(-4,0)、D(8,3)分别代入y=$\frac{1}{8}$x2+bx+c,得$\left\{\begin{array}{l}{2-4b+c=0}\\{8+8b+c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-\frac{1}{4}}\\{c=-3}\end{array}\right.$.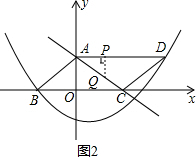
所以该二次函数的解析式为:y=$\frac{1}{8}$x2-$\frac{1}{4}$x-3;
(2)①设点P、Q运动的时间为t.
如图1,在△APQ中,AP=t,AQ=AC-CQ=5-t,cos∠PAQ=cos∠ACO=$\frac{4}{5}$.
当PQ⊥AC时,$\frac{AQ}{AP}$=$\frac{4}{5}$.所以$\frac{5-t}{t}$=$\frac{4}{5}$.
解得:t=$\frac{25}{9}$;
如图2,当QP⊥AD时.这时$\frac{AP}{AQ}$=$\frac{4}{5}$,所以$\frac{t}{5-t}$=$\frac{4}{5}$.解得:t=$\frac{20}{9}$.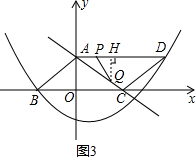
即AP=$\frac{25}{9}$或AP=$\frac{20}{9}$时,△APQ是直角三角形.
②如图3,过点Q作QH⊥AD,垂足为H.
由于S△APQ=$\frac{1}{2}$AP•QH=$\frac{1}{2}$AP•AQsin∠PAQ=$\frac{1}{2}$t(5-t)×$\frac{3}{5}$=-$\frac{3}{10}$t2+$\frac{3}{2}$t,
S△ACD=$\frac{1}{2}$AD•OA=$\frac{1}{2}$×8×3=12,
所以S四边形PDCQ=S△ACD-S△APQ=12-(-$\frac{3}{10}$t2+$\frac{3}{2}$t)=$\frac{3}{10}$(t-$\frac{5}{2}$)2+$\frac{81}{8}$.
所以当t=$\frac{5}{2}$,即AP=$\frac{5}{2}$时,四边形PDCQ的最小值是$\frac{81}{8}$.
点评 此题主要考查了二次函数综合以及直角三角形的性质以及二次函数最值求法等知识,利用数形结合以及分类讨论得出是解题关键.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(4,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(4,0),点A的纵坐标是1,则点B的坐标是( )| A. | (2,1) | B. | (2,-1) | C. | (1,-2) | D. | (1,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
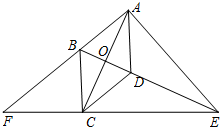 菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
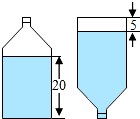 有种饮料瓶如图,它的直径是4cm,里面的水高度是20cm,把瓶盖拧紧倒置放平,无水部分圆柱高度是5cm,求饮料瓶的容积是多少?(结果保留整数)
有种饮料瓶如图,它的直径是4cm,里面的水高度是20cm,把瓶盖拧紧倒置放平,无水部分圆柱高度是5cm,求饮料瓶的容积是多少?(结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com