
【题目】如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点O,∠BAC=62°,∠C=70°,求∠EAD,∠BOE的度数分别是多少?

【答案】∠EAD=11°,∠BOE=55°.
【解析】
由AD⊥BC,可得∠ADC=90°,根据三角形内角和定理可得∠CAD=180°-90°-70°=20°,由于∠BAC=62°,AE是∠BAC的角平分线,可求出∠EAC=∠BAE=31°,继而求出∠EAD=∠EAC-∠CAD=31°-20°=11°,根据三角形内角和定理可得:∠ABC=180°-∠BAC-∠C=48°,由于BF是∠ABC的角平分线,可得∠ABO=24°,因此∠BOE=∠ABO+∠BAE=24°+31°=55°.
解∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°-90°-70°=20°,
∵∠BAC=62°,AE是∠BAC的角平分线,
∴∠EAC=∠BAE=31°,
∴∠EAD=∠EAC-∠CAD=31°-20°=11°,
∠ABC=180°-∠BAC-∠C=48°
∵BF是∠ABC的角平分线,
∴∠ABO=24°
∴∠BOE=∠ABO+∠BAE=24°+31°=55°.
故∠EAD,∠BOE的度数分别是11°,55°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
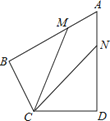
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=x和直线l2:y2=﹣2x+6相交于点A,直线l2与x轴交于点B,动点P沿路线O→A→B运动.
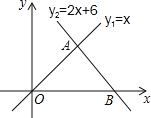
(1)求点A的坐标,并回答当x取何值时y1>y2?
(2)求△AOB的面积;
(3)当△POB的面积是△AOB的面积的一半时,求出这时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B,C分别在线段NM,NA上,在△ABC中,∠A∶∠ABC∶∠BCA=3∶5∶10,且△ABC≌△MNC,则∠BCM∶∠NBA等于( )
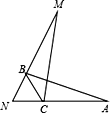
A.1∶2B.1∶3C.1∶4D.1∶5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.
(1) 用“列表法”或“树状图法”表示所有可能出现的结果;
(2) 小刚抽到物理实验B和化学实验F(记作事件P)的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90 ,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
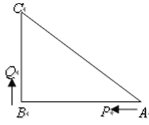
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com