
任意实数a,可用[a]表示不超过a的最大整数,如[4]=4,[ ]=1,现对72进行如下操作:72→[
]=1,现对72进行如下操作:72→[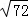 ]=8→[
]=8→[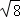 ]=2→[
]=2→[ ]=1,这样对72只需进行3次操作后变为1.类似地:对数字900进行了n次操作后变为1,那么n的值为( )
]=1,这样对72只需进行3次操作后变为1.类似地:对数字900进行了n次操作后变为1,那么n的值为( )
A. 3 B. 4 C. 5 D. 6
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:
已知函数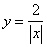 的图象在第一象限的一支曲线上有一点A(a,c+1),在该函数图象的另外一支上有点B(b,c),则关于一元二次方程ax2+bx+c=0的两根x1,x2判断正确的是( )
的图象在第一象限的一支曲线上有一点A(a,c+1),在该函数图象的另外一支上有点B(b,c),则关于一元二次方程ax2+bx+c=0的两根x1,x2判断正确的是( )
A.0<x1+x2<1,x1•x2>0 B.x1+x2<0,x1•x2>0
C.x1+x2>1,x1•x2>0 D.x1+x2与x1•x2的符号都不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠C=90°,∠B=32°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法:
①AD是∠BAC的平分线;
②CD是△ADC的高;
③点D在AB的垂直平分线上;
④∠ADC=61°.
其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
在△ABC中,AH⊥BC于点H,点P从B点开始出发向C点运动,在运动过程中,设线段AP的长为y,线段BP的长为x(如图1),而y关于x的函数图象如图2所示.Q (1,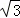 )是函数图象上的最低点.小明仔细观察图1,图2两图,作出如下结论:①AB=2;②AH=
)是函数图象上的最低点.小明仔细观察图1,图2两图,作出如下结论:①AB=2;②AH=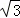 ;③AC=2
;③AC=2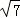 ;④x=2时,△ABP是等腰三角形;⑤若△ABP为钝角三角形,则0<x<1;其中正确的是 (填写序号).
;④x=2时,△ABP是等腰三角形;⑤若△ABP为钝角三角形,则0<x<1;其中正确的是 (填写序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
贵阳数博会于2015年5月26日至29日在贵阳国际会议展览中心举行,贵阳副市长刘春成介绍在近两年签约投资额已经超过了1.4×103多亿元.1.4×103这个数可以表示为( )
A. 14 B. 140 C. 1400 D. 14000
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过转转盘获得购物券.规定顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准100元、50元、20元的相应区域,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果指针对准其它区域,那么就不能获得购物券.另一种方式是:不转转盘,顾客每购买100元的商品,可直接获得10元购物券.据统计,一天中共有1000人次选择了转转盘的方式,其中指针落在100元、50元、20元的次数分别为50次、100次、200次.
(1)指针落在不获奖区域的概率约是多少?
(2)通过计算说明选择哪种方式更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com