
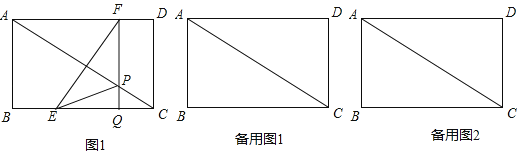
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,如果点E由点B出发沿BC方向向点C匀速运动,同时点F由点D出发沿DA方向向点A匀速运动,它们的速度分别为每秒2cm和1cm,FQ⊥BC,分别交AC、BC于点P和Q,设运动时间为t秒(0<t<4).
(1)连接EF,若运动时间t=![]() 秒时,求证:△EQF是等腰直角三角形;
秒时,求证:△EQF是等腰直角三角形;
(2)连接EP,当△EPC的面积为3cm2时,求t的值;
(3)在运动过程中,当t取何值时,△EPQ与△ADC相似.
【答案】(1)详见解析;(2)2秒;(3)2秒或![]() 秒或
秒或![]() 秒.
秒.
【解析】
(1)由题意通过计算发现EQ=FQ=6,由此即可证明;
(2)根据题意利用三角形的面积建立方程即可得出结论;
(3)由题意分点E在Q的左侧以及点E在Q的右侧这两种情况,分别进行分析即可得出结论.
解:(1)证明:若运动时间t=![]() 秒,则
秒,则
BE=2×![]() =
=![]() (cm),DF=
(cm),DF=![]() (cm),
(cm),
∵四边形ABCD是矩形
∴AD=BC=8(cm),AB=DC=6(cm),∠D=∠BCD=90°
∵∠D=∠FQC=∠QCD=90°,
∴四边形CDFQ也是矩形,
∴CQ=DF,CD=QF=6(cm),
∴EQ=BC﹣BE﹣CQ=8﹣![]() ﹣
﹣![]() =6(cm),
=6(cm),
∴EQ=QF=6(cm),
又∵FQ⊥BC,
∴△EQF是等腰直角三角形;
(2)由(1)知,CE=8﹣2t,CQ=t,
在Rt△ABC中,tan∠ACB=![]() =
=![]() ,
,
在Rt△CPQ中,tan∠ACB=![]() =
=![]() =
=![]() ,
,
∴PQ=![]() t,
t,
∵△EPC的面积为3cm2,
∴S△EPC=![]() CE×PQ=
CE×PQ=![]() ×(8﹣2t)×
×(8﹣2t)×![]() t=3,
t=3,
∴t=2秒,
即t的值为2秒;
(3)解:分两种情况:
Ⅰ.如图1中,点E在Q的左侧.
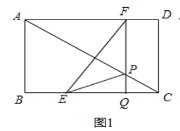
①∠PEQ=∠CAD时,△EQP∽△ADC,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠CAD=∠ACB,
∵△EQP∽△ADC,
∴∠CAD=∠QEP,
∴∠ACB=∠QEP,
∴EQ=CQ,
∴CE=2CQ,
由(1)知,CQ=t,CE=8-2t,
∴8-2t=2t,
∴t=2秒;
②∠PEQ=∠ACD时,△EPQ∽△CAD,
∴![]() ,
,
∵FQ⊥BC,
∴FQ∥AB,
∴△CPQ∽△CAB,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴ ,
,
解得:![]() ;
;
Ⅱ.如图2中,点E在Q的右侧.
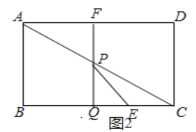
∵0<t<4,
∴点E不能与点C重合,
∴只存在△EPQ∽△CAD,
可得![]() ,即
,即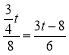 ,
,
解得:![]() ;
;
综上所述,t的值为2秒或![]() 秒或
秒或![]() 秒时,△EPQ与△ADC相似.
秒时,△EPQ与△ADC相似.


科目:初中数学 来源: 题型:
【题目】如图所示,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数y=![]() (x>0)的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连接OB1、OB2、OB3,若图中三个阴影部分的面积之和为
(x>0)的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连接OB1、OB2、OB3,若图中三个阴影部分的面积之和为![]() ,则k= .
,则k= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点A(2,0)的直线l与y轴交于点B,tan∠OAB=![]() ,直线l上的点P位于y轴左侧,且到y轴的距离为1.
,直线l上的点P位于y轴左侧,且到y轴的距离为1.
(1)求直线l的表达式;
(2)若反比例函数![]() 的图象经过点P,求m的值.
的图象经过点P,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
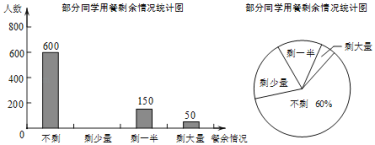
(1)这次被调查的同学共有 人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() 与x轴交于A、B两点,△ABC为等边三角形,∠COD=60°,且OD=OC.
与x轴交于A、B两点,△ABC为等边三角形,∠COD=60°,且OD=OC.
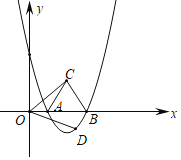
(1)A点坐标为 ,B点坐标为 ;
(2)求证:点D在抛物线上;
(3)点M在抛物线的对称轴上,点N在抛物线上,若以M、N、O、D为顶点的四边形为平行四边形,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
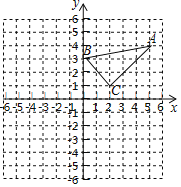
(1)画出△ABC关于原点成中心对称的△A1B1C1,并写出点C1的坐标;
(2)画出将A1B1C1绕点C1按顺时针旋转90°所得的△A2B2C1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=3,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则四边形ABEF的周长为( )
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则四边形ABEF的周长为( )
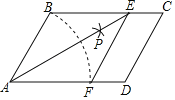
A.12B.14C.16D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )

A. 12 B. 6 C. 6![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
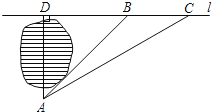
【题目】如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据 tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com