练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路．现新修一条路AC到公路l．小明测量出∠ACD＝31°，∠ABD＝45°，BC＝50m．请你帮小明计算他家到公路l的距离AD的长度？（精确到0.1m；参考数据 tan31°≈0.60，sin31°≈0.51，cos31°≈0.86）．

    【答案】75.0m

    【解析】

    设BD=AD=xm，利用x表示出CD的长，然后在直角△ACD中，利用三角函数即可得到AD和CD的比值，即可列方程求得x的值．

    ∵∠ADB=90°，∠ABD＝45°，

    ∴ ∠DAB=45°，
    ∴∠ABD＝∠DAB，

    ∴BD=AD
    设BD=AD=xm，
    ∵BC=50m
    ∴CD=x+50，
    在Rt△ACD中
    tanC=，
    即


    答：AD的长度75.0m．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

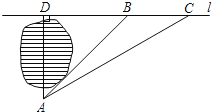
    【题目】如图1，在矩形ABCD中，AB＝6cm，BC＝8cm，如果点E由点B出发沿BC方向向点C匀速运动，同时点F由点D出发沿DA方向向点A匀速运动，它们的速度分别为每秒2cm和1cm，FQ⊥BC，分别交AC、BC于点P和Q，设运动时间为t秒（0＜t＜4）．

    （1）连接EF，若运动时间t＝秒时，求证：△EQF是等腰直角三角形；

    （2）连接EP，当△EPC的面积为3cm2时，求t的值；

    （3）在运动过程中，当t取何值时，△EPQ与△ADC相似．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

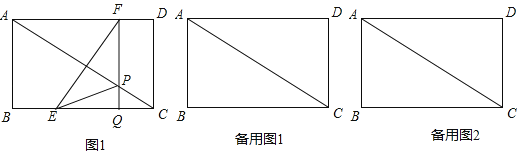
    【题目】如图，AB是⊙O的直径，⊙O过AC的中点D，DE切⊙O于点D，交BC于E．

    （1）求证DE⊥BC；

    （2）若⊙O的半径为5，BE＝2，求DE的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

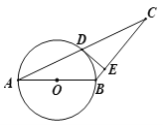
    【题目】如图所示，正方形ABCD中，BE=EF=FC，CG=2GD，BG分别交AE，AF于M，N，下列结论：①AF⊥BG；②BN=NF；③；④S四边形CGNF=S四边形ANGD．其中正确的结论的序号是（　　）

    A.①③B.②④C.①②D.③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

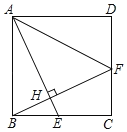
    【题目】如图，正方形ABCD中，E是BC上的一点，连接AE，过B点作BH⊥AE，垂足为点H，延长BH交CD于点F，连接AF．

    （1）求证：AE=BF；

    （2）若正方形边长为5，BE=2，求sin∠DAF的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

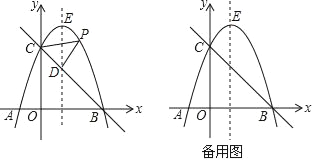
    【题目】如图，在平面直角坐标系中，抛物线y＝ax2+2x+c与x轴交A（﹣1，0），B两点，与y轴交于点C（0，3），抛物线的顶点为点E．

    (1)求抛物线的解析式；

    (2)经过B，C两点的直线交抛物线的对称轴于点D，点P为直线BC上方抛物线上的一个动点，当点P运动到点E时，求△PCD的面积；

    (3)点N在抛物线对称轴上，点M在x轴上，是否存在这样的点M与点N，使以M，N，C，B为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标（不写求解过程）；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，线段AB经过旋转变换得到线段A1B1，A的对应点为A1，B的对应点为B1．

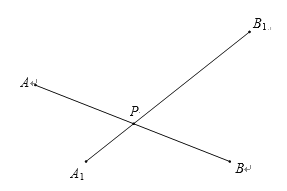
    （1）在图中画出旋转中心O；

    （2）设线段AB和线段A1B1交于点P，线段AB逆时针旋转的最小旋转角为，若∠APB1 ，请直接写出，满足的等量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形中，，，是边上一点，将沿直线对折，得到．

    （1）当平分时，求的长；

    （2）连接，当，求的面积；

    （3）当射线交于点时，求的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数图象的顶点坐标为，且过点，

    （1）求抛物线的解析式；

    （2）当时，求的取值范围．

    查看答案和解析>>

    同步练习册答案