
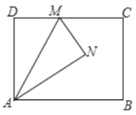
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是边
是边![]() 上一点,将
上一点,将![]() 沿直线
沿直线![]() 对折,得到
对折,得到![]() .
.
(1)当![]() 平分
平分![]() 时,求
时,求![]() 的长;
的长;
(2)连接![]() ,当
,当![]() ,求
,求![]() 的面积;
的面积;
(3)当射线![]() 交
交![]() 于点
于点![]() 时,求
时,求![]() 的最大值.
的最大值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由折叠性质得∠MAN=∠DAM,证出∠DAM=∠MAN=∠NAB,由三角函数得出DM=ADtan∠DAM=![]() 即可;
即可;
(2)延长MN交AB延长线于点Q,由矩形的性质得出∠DMA=∠MAQ,由折叠性质得出∠DMA=∠AMQ,AN=AD=3,MN=MD=1,得出∠MAQ=∠AMQ,证出MQ=AQ,设NQ=x,则AQ=MQ=1+x,证出∠ANQ=90°,在Rt△ANQ中,由勾股定理得出方程,解方程求出NQ=4,AQ=5,即可求出△ABN的面积;
(3)过点A作AH⊥BF于点H,证明△ABH∽△BFC,得出对应边成比例![]() ,得出当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,由折叠性质得:AD=AH,由AAS证明△ABH≌△BFC,得出CF=BH,由勾股定理求出BH,得出CF,即可得出结果.
,得出当点N、H重合(即AH=AN)时,AH最大,BH最小,CF最小,DF最大,此时点M、F重合,B、N、M三点共线,由折叠性质得:AD=AH,由AAS证明△ABH≌△BFC,得出CF=BH,由勾股定理求出BH,得出CF,即可得出结果.
解:(1)由折叠性质得:![]() ,
,
![]() ,
,
![]() 平分
平分![]() ,
,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,
![]() ;
;
(2)延长![]() 交
交![]() 延长线于点
延长线于点![]() ,如图1所示:
,如图1所示:
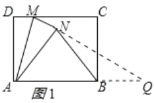
![]() 四边形
四边形![]() 是矩形
是矩形
![]() ,
,
![]() ,
,
由折叠性质得:![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ;
;
(3)过点![]() 作
作![]() 于点
于点![]() ,如图2所示:
,如图2所示:
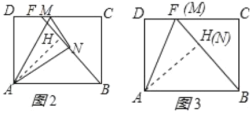
![]() 四边形
四边形![]() 是矩形
是矩形
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 可以看到点
可以看到点![]() 是在以
是在以![]() 为圆心3为半径的圆上运动,所以当射线
为圆心3为半径的圆上运动,所以当射线![]() 与圆相切时,
与圆相切时,![]() 最大,此时
最大,此时![]() 、
、![]() 、
、![]() 三点共线,如图3所示
三点共线,如图3所示
由折叠性质得:![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,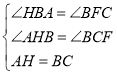 ,
,
![]() ,
,
![]() ,
,
由勾股定理得:![]() ,
,
![]() ,
,
![]() 的最大值
的最大值![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )

A. 12 B. 6 C. 6![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据 tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
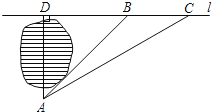
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一根直尺短边长![]() ,长边长
,长边长![]() ,还有一块锐角为45°的直角三角形纸板,它的斜边长为
,还有一块锐角为45°的直角三角形纸板,它的斜边长为![]() .如图1,将直尺的短边
.如图1,将直尺的短边![]() 与直角三角形纸板的斜边
与直角三角形纸板的斜边![]() 重合,且点
重合,且点![]() 与点
与点![]() 重合.将直尺沿射线
重合.将直尺沿射线![]() 方向平移,如图2,设平移的长度为
方向平移,如图2,设平移的长度为![]() ,且满足
,且满足![]() ,直尺和三角形纸板重叠部分的面积为
,直尺和三角形纸板重叠部分的面积为![]() .
.
(1)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(2)当![]() 时(如图3),请用含
时(如图3),请用含![]() 的代数式表示
的代数式表示![]() .
.
(3)是否存在一个位置,使重叠部分面积为![]() ?若存在求出此时
?若存在求出此时![]() 的值.
的值.
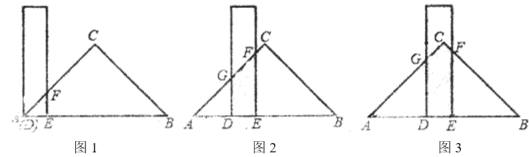
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,关于x的二次函数y=ax2﹣2ax(a>0)的顶点为C,与x轴交于点O、A,关于x的一次函数y=﹣ax(a>0).
(1)试说明点C在一次函数的图象上;
(2)若两个点(k,y1)、(k+2,y2)(k≠0,±2)都在二次函数的图象上,是否存在整数k,满足![]() ?如果存在,请求出k的值;如果不存在,请说明理由;
?如果存在,请求出k的值;如果不存在,请说明理由;
(3)若点E是二次函数图象上一动点,E点的横坐标是n,且﹣1≤n≤1,过点E作y轴的平行线,与一次函数图象交于点F,当0<a≤2时,求线段EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() .
.

(1)如图1,当![]() 时,求证:
时,求证:![]() ;
;
(2)当![]() 时.
时.
①如图2,猜想线段![]() 、
、![]() 之间的数量关系,并证明你的猜想;
之间的数量关系,并证明你的猜想;
②如图3,点![]() 时
时![]() 边的中点,连接
边的中点,连接![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科研小组计划对某一品种的西瓜用两种种植技术种植.在选择种植技术时,该科研小组主要关心的问题是:西瓜的产量和产量的稳定性,以及西瓜的优等品率.为了解这两种种植技术种出的西瓜的质量情况,科研小组各对两块自然条件相同的试验田进行对比试验,并从这两块实验田中随机抽取20个西瓜,分别称重后,将称重的结果记录如下:
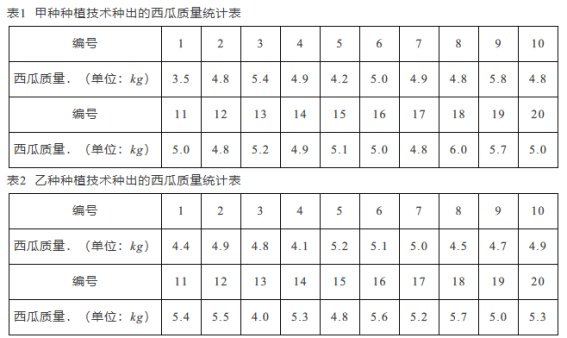
回答下列问题:
(1)若将质量为4.5~5.5(单位:kg)的西瓜记为优等品,完成下表:
优等品西瓜个数 | 平均数 | 方差 | |
甲种种植技术种出的西瓜质量 | 4.98 | 0.27 | |
乙种种植技术种出的西瓜质量 | 15 | 4.97 | 0.21 |
(2)根据以上数据,你认为该科研小组应选择哪种种植技术?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“距离”,记作![]() 特别地,若图形M,N有公共点,规定
特别地,若图形M,N有公共点,规定![]() .
.

![]() 如图1,
如图1,![]() 的半径为2,
的半径为2,
![]() 点
点![]() ,
,![]() ,则
,则![]() ______,
______,![]() ______.
______.
![]() 已知直线l:
已知直线l:![]() 与
与![]() 的“距离”
的“距离”![]() ,求b的值.
,求b的值.
![]() 已知点
已知点![]() ,
,![]() ,
,![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() 若
若![]() ,请直接写出m的取值范围______.
,请直接写出m的取值范围______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是反比例函数![]() (k≠0)图象上的两点,延长线段AB交y轴于点C,且B为线段AC的中点,过点A作AD⊥x轴于点D,E为线段OD的三等分点,且OE<DE.连接AE,BE.若S△ABE=7,则k的值为_________.
(k≠0)图象上的两点,延长线段AB交y轴于点C,且B为线段AC的中点,过点A作AD⊥x轴于点D,E为线段OD的三等分点,且OE<DE.连接AE,BE.若S△ABE=7,则k的值为_________.
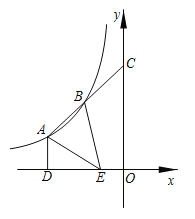
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com