
【题目】在平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“距离”,记作![]() 特别地,若图形M,N有公共点,规定
特别地,若图形M,N有公共点,规定![]() .
.

![]() 如图1,
如图1,![]() 的半径为2,
的半径为2,
![]() 点
点![]() ,
,![]() ,则
,则![]() ______,
______,![]() ______.
______.
![]() 已知直线l:
已知直线l:![]() 与
与![]() 的“距离”
的“距离”![]() ,求b的值.
,求b的值.
![]() 已知点
已知点![]() ,
,![]() ,
,![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() 若
若![]() ,请直接写出m的取值范围______.
,请直接写出m的取值范围______.
【答案】(1)![]() 1 , 3,
1 , 3,![]() ;(2)m的值为
;(2)m的值为![]() 或
或![]() 或
或![]() .
.
【解析】
![]() 根据图形M,N间的“距离”的定义即可解决问题;
根据图形M,N间的“距离”的定义即可解决问题;
![]() 设直线l交x轴,y轴于点P,Q,作
设直线l交x轴,y轴于点P,Q,作![]() 于H,OH交
于H,OH交![]() 于
于![]() 根据
根据![]() 与
与![]() 的“距离”
的“距离”![]() ,构建方程即可解决问题;
,构建方程即可解决问题;
![]() 如图2中,设AC交x轴于
如图2中,设AC交x轴于![]() 分四种情形分别求解即可解决问题.
分四种情形分别求解即可解决问题.
![]() 如图1中,连接OB交
如图1中,连接OB交![]() 于点E,设
于点E,设![]() 交y轴于点F.
交y轴于点F.

由题意:![]() ,
,![]() ,
,
故答案为1,3.
![]() 如图1中,设直线l交x轴,y轴于点P,Q,作
如图1中,设直线l交x轴,y轴于点P,Q,作![]() 于H,OH交
于H,OH交![]() 于G.
于G.
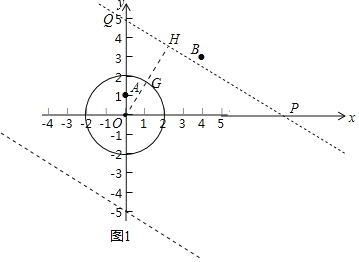
由题意:![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线l:
直线l:![]() 与
与![]() 的“距离”
的“距离”![]() ,
,
![]() ,
,
![]() .
.
![]() 如图2中,设AC交x轴于E.
如图2中,设AC交x轴于E.
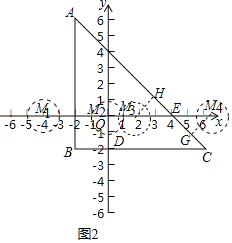
![]() ,
,
![]() 当
当![]() 时,
时,![]() 满足条件,
满足条件,
当![]() 时,
时,![]() 满足条件,
满足条件,
假设![]() 满足条件,作
满足条件,作![]() ,
,
由题意![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
观察图象可知:当![]() 时,
时,![]() 满足条件,
满足条件,
假设![]() 满足条件,作
满足条件,作![]() 于G,
于G,
由题意;![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
综上所述,满足条件的m的值为![]() 或
或![]() 或
或![]() .
.
故答案为4或![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N,下列结论:①AF⊥BG;②BN=![]() NF;③
NF;③![]() ;④S四边形CGNF=
;④S四边形CGNF=![]() S四边形ANGD.其中正确的结论的序号是( )
S四边形ANGD.其中正确的结论的序号是( )
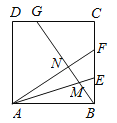
A.①③B.②④C.①②D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图.请结合图中所给的信息解答下列问题:
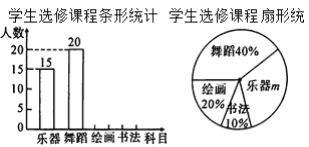
(1)本次调查的学生共有______人,在扇形统计图中,m的值是______,将条形统计图补充完整;
(2)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现在要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请画树状图或列表求出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
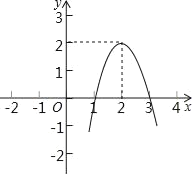
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k是常数,抛物线y=x2+(k2+k-6)x+3k的对称轴是y轴,并且与x轴有两个交点.
(1)求k的值:
(2)若点P在抛物线y=x2+(k2+k-6)x+3k上,且P到y轴的距离是2,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书籍是人类进步的阶梯.联合国教科文组织把每年的4月23日确定为“世界读书日”.某校为了了解该校学生一个学期阅读课外书籍的情况,在全校范围内随机对100名学生进行了问卷调查,根据调查的结果,绘制了统计图表的一部分:一个学期平均一天阅读课外书籍所有时间统计表
时间(分钟) | 20 | 40 | 60 | 80 | 100 | 120 |
人数(名) | 43 | 31 | 15 | 5 | 4 | 2 |
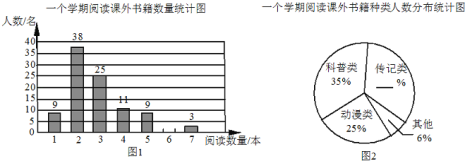
请你根据以上信息解答下列问题:
(1)补全图1、图2;
(2)这100名学生一个学期平均每人阅读课外书籍多少本?若该校共有4000名学生,请你估计这个学校学生一个学期阅读课外书籍共多少本?
(3)根据统计表,求一个学期平均一天阅读课外书籍所用时间的众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,顶点为
,顶点为![]() .
.
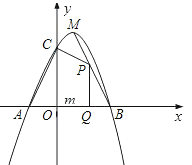
(1)求二次函数的解析式;
(2)点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() ,若
,若![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)探索:线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?如果存在,求出点
为等腰三角形?如果存在,求出点![]() 的坐标;如果不存在,请说呀理由.
的坐标;如果不存在,请说呀理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com