
【题目】书籍是人类进步的阶梯.联合国教科文组织把每年的4月23日确定为“世界读书日”.某校为了了解该校学生一个学期阅读课外书籍的情况,在全校范围内随机对100名学生进行了问卷调查,根据调查的结果,绘制了统计图表的一部分:一个学期平均一天阅读课外书籍所有时间统计表
时间(分钟) | 20 | 40 | 60 | 80 | 100 | 120 |
人数(名) | 43 | 31 | 15 | 5 | 4 | 2 |
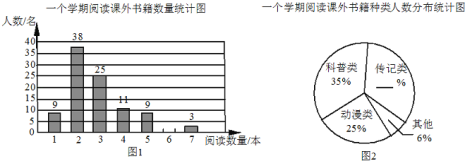
请你根据以上信息解答下列问题:
(1)补全图1、图2;
(2)这100名学生一个学期平均每人阅读课外书籍多少本?若该校共有4000名学生,请你估计这个学校学生一个学期阅读课外书籍共多少本?
(3)根据统计表,求一个学期平均一天阅读课外书籍所用时间的众数和中位数.
【答案】(1)见解析;(2)3本,12000本;(3)众数为20分钟,中位数为40分钟
【解析】
(1)利用总人数100求出阅读6本是人数,根据总百分比1求出传记类的百分比,即可补全图形;
(2)先根据加权平均数公式求出平均阅读的本数,即可得到全校的阅读数量;
(3)根据阅读时间的表格即可得到答案.
解:(1)根据题意得:100﹣(9+38+25+11+9+3)=5(人);1﹣(35%+25%+6%)=34%,
补全图形,如图所示;
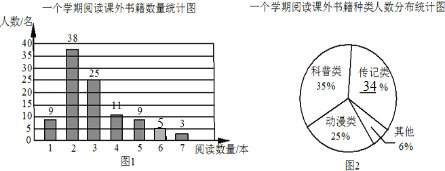
(2)根据题意得:![]() =3(本),
=3(本),
则这100名学生一个学期平均每人阅读课外书籍3本;
根据题意得:3×4000=12000(本),
则估计这个学校学生一个学期阅读课外书籍共12000本;
(3)根据表格得:众数为20分钟,中位数为40分钟.


科目:初中数学 来源: 题型:
【题目】有一根直尺短边长![]() ,长边长
,长边长![]() ,还有一块锐角为45°的直角三角形纸板,它的斜边长为
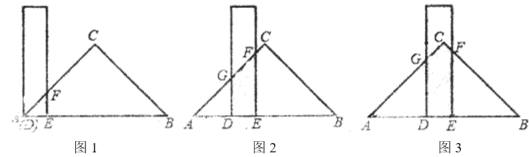
,还有一块锐角为45°的直角三角形纸板,它的斜边长为![]() .如图1,将直尺的短边
.如图1,将直尺的短边![]() 与直角三角形纸板的斜边
与直角三角形纸板的斜边![]() 重合,且点
重合,且点![]() 与点
与点![]() 重合.将直尺沿射线
重合.将直尺沿射线![]() 方向平移,如图2,设平移的长度为
方向平移,如图2,设平移的长度为![]() ,且满足
,且满足![]() ,直尺和三角形纸板重叠部分的面积为
,直尺和三角形纸板重叠部分的面积为![]() .
.
(1)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(2)当![]() 时(如图3),请用含
时(如图3),请用含![]() 的代数式表示
的代数式表示![]() .
.
(3)是否存在一个位置,使重叠部分面积为![]() ?若存在求出此时
?若存在求出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“距离”,记作![]() 特别地,若图形M,N有公共点,规定
特别地,若图形M,N有公共点,规定![]() .
.

![]() 如图1,
如图1,![]() 的半径为2,
的半径为2,
![]() 点
点![]() ,
,![]() ,则
,则![]() ______,
______,![]() ______.
______.
![]() 已知直线l:
已知直线l:![]() 与
与![]() 的“距离”
的“距离”![]() ,求b的值.
,求b的值.
![]() 已知点
已知点![]() ,
,![]() ,
,![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() 若
若![]() ,请直接写出m的取值范围______.
,请直接写出m的取值范围______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某企业安排![]() 名工人生产甲、乙两种产品,每人每天生产
名工人生产甲、乙两种产品,每人每天生产![]() 件甲或
件甲或![]() 件乙,甲产品每件可获利
件乙,甲产品每件可获利![]() 元.根据市场需求和生产经验,乙产品每天产量不少于
元.根据市场需求和生产经验,乙产品每天产量不少于![]() 件,当每天生产
件,当每天生产![]() 件时,每件可获利
件时,每件可获利![]() 元, 每增加
元, 每增加![]() 件,当天平均每件利润减少
件,当天平均每件利润减少![]() 元.设每天安排
元.设每天安排![]() 人生产乙产品.
人生产乙产品.
![]() 根据信息填表:
根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | __________ | _____________ |
|
乙 |
|
| _____________ |
![]() 若每天生产甲产品可获得的利润比生产乙产品可获得的利润多
若每天生产甲产品可获得的利润比生产乙产品可获得的利润多![]() 元,求每件乙产品可获得的利润.
元,求每件乙产品可获得的利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
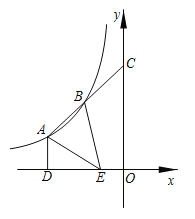
【题目】如图,A,B是反比例函数![]() (k≠0)图象上的两点,延长线段AB交y轴于点C,且B为线段AC的中点,过点A作AD⊥x轴于点D,E为线段OD的三等分点,且OE<DE.连接AE,BE.若S△ABE=7,则k的值为_________.
(k≠0)图象上的两点,延长线段AB交y轴于点C,且B为线段AC的中点,过点A作AD⊥x轴于点D,E为线段OD的三等分点,且OE<DE.连接AE,BE.若S△ABE=7,则k的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于
轴分别相交于![]() 、
、![]() 两点;分别过
两点;分别过![]() 、
、![]() 两点作
两点作![]() 轴、
轴、![]() 轴的垂线相交于
轴的垂线相交于![]() 点.
点.![]() 为
为![]() 边上一动点.
边上一动点.
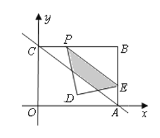
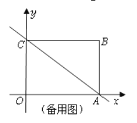
(1)求三角形![]() 的面积;
的面积;
(2)点![]() 从点
从点![]() 出发沿着
出发沿着![]() 以每秒1个单位长度的速度向点
以每秒1个单位长度的速度向点![]() 匀速运动,过点
匀速运动,过点![]() 作
作![]() 交
交![]() 于
于![]() ,设运动时间为
,设运动时间为![]() 秒.用含
秒.用含![]() 的代数式表示
的代数式表示![]() 的面积
的面积![]() ;
;
(3)在(2)的条件下点![]() 的运动过程中,将
的运动过程中,将![]() 沿着
沿着![]() 折叠(如图所示),点
折叠(如图所示),点![]() 在平面内的落点为点
在平面内的落点为点![]() .当
.当![]() 与
与![]() 重叠部分的面积等于
重叠部分的面积等于![]() 时,试求出
时,试求出![]() 点的横坐标.
点的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙C的半径为2,圆外一点O满足OC=3.5,点P为⊙C上一动点,经过点O的直线l上有两点A、B,且OA=OB,∠APB=90°,l不经过点C,则AB的最小值为( )
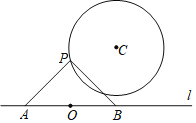
A. 2 B. 2.5 C. 3 D. 3.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com