
【题目】如图所示,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N,下列结论:①AF⊥BG;②BN=![]() NF;③
NF;③![]() ;④S四边形CGNF=
;④S四边形CGNF=![]() S四边形ANGD.其中正确的结论的序号是( )
S四边形ANGD.其中正确的结论的序号是( )
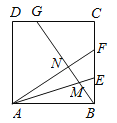
A.①③B.②④C.①②D.③④
【答案】A
【解析】
①利用SAS证△ABF≌△BCG即可进行判断;
②证明△BNF∽△BCG,求得![]() 的值,即可判断;
的值,即可判断;
③作EH⊥AF,令AB=3,分别求得MN,BM的值,即可判断;
④连接AG,FG,根据③中结论分别求得S四边形CGNF和S四边形ANGD即可.
解:①∵四边形ABCD为正方形,∴AB=BC=CD,
∵BE=EF=FC,CG=2GD,∴BF=CG,
在△ABF和△BCG中,
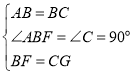 ,
,
∴△ABF≌△BCG,
∴∠BAF=∠CBG,
∵∠BAF+∠BFA=90°,
∴∠CBG+∠BFA=90°,即AF⊥BG;所以①正确;
②在△BNF和△BCG中,∠CBG=∠NBF,∠C=∠BNF=90°,
∴△BNF∽△BCG,∴![]() ,
,
∴BN=![]() NF;所以②错误;
NF;所以②错误;
③作EH⊥AF,令AB=3,则BF=2,BE=EF=CF=1,
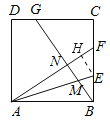
AF=![]() ,
,
∵S△ABF=![]() AFBN=
AFBN=![]() ABBF,
ABBF,
∴BN=![]() ,NF=
,NF=![]() BN=
BN=![]() ,
,
∴AN=AF﹣NF=![]() ,
,
∵E是BF中点,
∴EH是△BFN的中位线,
∴EH=![]() ,NH=
,NH=![]() ,BN∥EH,
,BN∥EH,
∴AH=![]() ,
,![]() ,解得:MN=
,解得:MN=![]() ,
,
∴BM=BN﹣MN=![]() ,MG=BG﹣BM=
,MG=BG﹣BM=![]() ,
,
∴![]() ;所以③正确;
;所以③正确;
④连接AG,FG,根据③中结论,
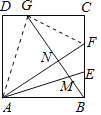
则NG=BG﹣BN=![]() ,
,
∵S四边形CGNF=S△CFG+S△GNF=![]() CGCF+
CGCF+![]() NFNG=1+
NFNG=1+![]() =
=![]() ,
,
S四边形ANGD=S△ANG+S△ADG=![]() ANGN+
ANGN+![]() ADDG=
ADDG=![]() ,
,
∴S四边形CGNF≠![]() S四边形ANGD,所以④错误.
S四边形ANGD,所以④错误.
故选A.


科目:初中数学 来源: 题型:
【题目】某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如图所示的不完整的统计图.
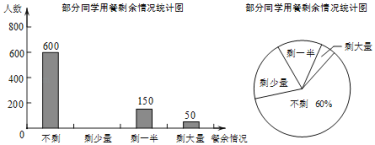
(1)这次被调查的同学共有 人;
(2)补全条形统计图,并在图上标明相应的数据;
(3)校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供50人食用一餐.据此估算,该校18000名学生一餐浪费的食物可供多少人食用一餐.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )

A. 12 B. 6 C. 6![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育看台侧面的示意图如图所示,观众区AC的坡度i为1:2,顶端C离水平地面AB的高度为10m,从顶棚的D处看E处的仰角α=18°30′,竖直的立杆上C、D两点间的距离为4m,E处到观众区底端A处的水平距离AF为3m.
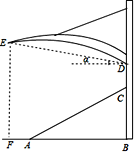
求:(1)观众区的水平宽度AB;
(2)顶棚的E处离地面的高度EF.(sin18°30′≈0.32,tanl8°30′≈0.33,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(m﹣2)x2+2mx+m﹣3的图象与x轴有两个交点,(x1,0),(x2,0),则下列说法正确是( )
①该函数图象一定过定点(﹣1,﹣5);
②若该函数图象开口向下,则m的取值范围为:![]() m<2;
m<2;
③当m>2,且1≤x≤2时,y的最大值为:4m﹣5;
④当m>2,且该函数图象与x轴两交点的横坐标x1,x2满足﹣3<x1<﹣2,﹣1<x2<0时,m的取值范围为:![]() m<11.
m<11.
A.①②③④B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=0.4m,EF=0.2m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高。
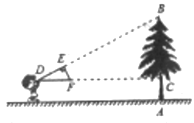
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据 tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
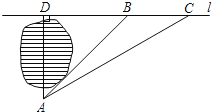
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一根直尺短边长![]() ,长边长
,长边长![]() ,还有一块锐角为45°的直角三角形纸板,它的斜边长为
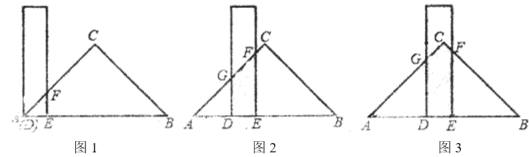
,还有一块锐角为45°的直角三角形纸板,它的斜边长为![]() .如图1,将直尺的短边
.如图1,将直尺的短边![]() 与直角三角形纸板的斜边
与直角三角形纸板的斜边![]() 重合,且点
重合,且点![]() 与点
与点![]() 重合.将直尺沿射线
重合.将直尺沿射线![]() 方向平移,如图2,设平移的长度为
方向平移,如图2,设平移的长度为![]() ,且满足
,且满足![]() ,直尺和三角形纸板重叠部分的面积为
,直尺和三角形纸板重叠部分的面积为![]() .
.
(1)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(2)当![]() 时(如图3),请用含
时(如图3),请用含![]() 的代数式表示
的代数式表示![]() .
.
(3)是否存在一个位置,使重叠部分面积为![]() ?若存在求出此时
?若存在求出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中的图形M,N,给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P,Q两点间的距离有最小值,那么称这个最小值为图形M,N间的“距离”,记作![]() 特别地,若图形M,N有公共点,规定
特别地,若图形M,N有公共点,规定![]() .
.

![]() 如图1,
如图1,![]() 的半径为2,
的半径为2,
![]() 点
点![]() ,
,![]() ,则
,则![]() ______,
______,![]() ______.
______.
![]() 已知直线l:
已知直线l:![]() 与
与![]() 的“距离”
的“距离”![]() ,求b的值.
,求b的值.
![]() 已知点
已知点![]() ,
,![]() ,
,![]() 的圆心为
的圆心为![]() ,半径为
,半径为![]() 若
若![]() ,请直接写出m的取值范围______.
,请直接写出m的取值范围______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com