
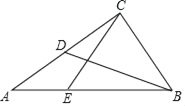
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,BC=![]() ,cot∠ABC=
,cot∠ABC=![]() ,点D是AC的中点.
,点D是AC的中点.
(1)求线段BD的长;
(2)点E在边AB上,且CE=CB,求△ACE的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据直角三角的特点,由∠ABC的正切值求出AC的长,然后根据中点的性质求出CD,再根据勾股定理可求解;
(2)过C作CH⊥AB于H,构造直角三角形,然后根据锐角三角函数求解.
试题解析:(1)Rt△ABC中,∠ACB=90°,BC=![]() ,cot∠ABC=
,cot∠ABC=![]() ,
,
∴AC=![]() ,
,
∵点D是AC的中点,
∴CD=![]() AC=
AC=![]() ,
,
∴Rt△BCD中,BD=![]() =
=![]() ;
;
(2)如图,过C作CH⊥AB于H,
∵BC=![]() ,cot∠ABC=
,cot∠ABC=![]() ,
,
∴CH=![]() ,BH=2,
,BH=2,
∵CE=CB,
∴EH=BH=1,
∵∠ACB=90°,BC=![]() ,AC=
,AC=![]() ,
,
∴AB=3,
∴AE=3﹣2=1,
∴△ACE的面积=![]() ×AE×CH=
×AE×CH=![]() ×1×
×1×![]() =
=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】黄山位于安徽省南部,是世界文化与自然双重遗产,世界地质公园,国家![]() 级旅游景区,全国文明风景旅游区示范点,中华十大名山,天下第一奇山.
级旅游景区,全国文明风景旅游区示范点,中华十大名山,天下第一奇山.
暑假期间,太和县某学校组织七年级学生到黄山游学,如果租用甲种客车2辆,乙种客车3辆,则可载180人,如果租用甲种客车3辆,乙种客车1辆,则可载165人.
(1)请问甲、乙两种客车每辆分别能载客多少人?
(2)若该学校七年级有303名学生参加这次游学活动,学校计划每辆车安排一名老师,老师也需一个座位.
①现打算同时租甲、乙两种客车共8辆,请帮助学校设计租车方案.
②旅行前,学校的一名老师由于特殊情况,学校只能安排7名老师,为保证所租的每辆车均有一名老师,租车方案调整为:同时租65座、45座和30座的大小三种客车,出发时,所租的三种客车的座位恰好坐满,请问学校的租车方案如何安排?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
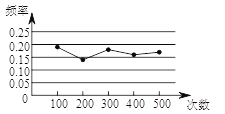
A. 袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球
B. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
C. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 y=-2x+5 的图像分别与 x 轴,y 轴交于点A、B,以线段AB 为边在第一象限内作等腰 RtABC,BAC=90 ,求过 B、C 两点的直线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() 是整数).
是整数).
⑴.求证:方程有两个不相等的实数根;
⑵.若方程的两个实数根分别为![]() (其中
(其中![]() ),设
),设![]() ,判断
,判断![]() 是否为变量
是否为变量![]() 的函数?如果是,请写出函数表达式;若不是,请说明理由.
的函数?如果是,请写出函数表达式;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)求值:![]()
(2)用消元法解方程组 时,两位同学的解法如下:
时,两位同学的解法如下:
解法一:
由①-②,得![]() .
.
解法二:
由②得,![]() ,③
,③
把①代入③,得![]() .
.
①反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“×”.
②请选择一种你喜欢的方法,完成解答.
(3)求不等式组 的正整数解.
的正整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A为钝角,AB=20cm,AC=12cm,点P从点B出发以3cm/s的速度向点A运动,点Q同时从点A出发以2cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动.当△APQ是等腰三角形时,运动的时间是( )
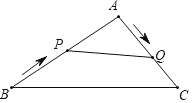
A.2.5sB.3sC.3.5sD.4s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列证明过程填空,请在括号里面填写对应的推理的理由.如图,已知:直线AB、CD被直线BC所截;直线BC、DE被直线CD所截,∠1+∠2 =180°,且∠1=∠D,求证:BC∥DE.
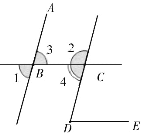
证明:∵∠1+∠2=180°(已知)
又∵∠1=∠3 .
∴∠2+∠3=180°(等量代换)
∴AB∥ .
∴∠4=∠1 .
又∵∠1=∠D .
∴∠D= (等量代换)
∴BC∥DE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
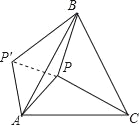
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com