
【题目】黄山位于安徽省南部,是世界文化与自然双重遗产,世界地质公园,国家![]() 级旅游景区,全国文明风景旅游区示范点,中华十大名山,天下第一奇山.
级旅游景区,全国文明风景旅游区示范点,中华十大名山,天下第一奇山.
暑假期间,太和县某学校组织七年级学生到黄山游学,如果租用甲种客车2辆,乙种客车3辆,则可载180人,如果租用甲种客车3辆,乙种客车1辆,则可载165人.
(1)请问甲、乙两种客车每辆分别能载客多少人?
(2)若该学校七年级有303名学生参加这次游学活动,学校计划每辆车安排一名老师,老师也需一个座位.
①现打算同时租甲、乙两种客车共8辆,请帮助学校设计租车方案.
②旅行前,学校的一名老师由于特殊情况,学校只能安排7名老师,为保证所租的每辆车均有一名老师,租车方案调整为:同时租65座、45座和30座的大小三种客车,出发时,所租的三种客车的座位恰好坐满,请问学校的租车方案如何安排?
【答案】(1)甲种客车每辆能载客45人,乙种客车每辆能载客30人;(2)①有三种租车方案:a租甲种客车5辆,则租乙种客车3辆;b租甲种客车6辆,则租乙种客车2辆;c租甲种客车7辆,则租乙种客车1辆;②租车方案为:租65座的客车2辆,45座的客车2辆,30座的3辆.
【解析】
(1)设甲种客车每辆能载客x人,乙两种客车每辆能载客x人,根据租用甲种客车2辆,乙种客车3辆,则可载180人,如果租用甲种客车3辆,乙种客车1辆,则可载165人,列出方程组解答即可;
(2)①设租甲种客车a辆,则租乙种客车(8a)辆,根据题意列出不等式解答即可;
②设同时租65座、45座和30座的大小三种客车各m辆,n辆,(7mn)辆,根据总人数列出方程解答即可.
解:(1)设甲种客车每辆能载客![]() 人,乙种客车每辆能载客
人,乙种客车每辆能载客![]() 人,
人,
根据题意得![]() ,解得:
,解得:![]()
答:甲种客车每辆能载客45人,乙种客车每辆能载客30人;
(2)①设租甲种客车![]() 辆,则租乙种客车
辆,则租乙种客车![]() 辆,
辆,
依题意得![]() ,解得
,解得![]()
∵打算同时租甲、乙两种客车,∴![]()
有三种租车方案:
a.租甲种客车5辆,则租乙种客车3辆;
b.租甲种客车6辆,则租乙种客车2辆;
c.租甲种客车7辆,则租乙种客车1辆.;
②设同时租65座、45座和30座的大小三种客车各![]() 辆,
辆,![]() 辆,
辆,![]() 辆,
辆,
根据题意得出:![]() ,
,
整理得出:![]() ,
,
故符合题意的有:![]() ,
,![]() ,
,![]() ,
,
租车方案为:租65座的客车2辆,45座的客车2辆,30座的3辆.


科目:初中数学 来源: 题型:
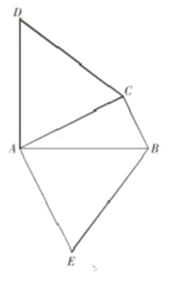
【题目】如图,在△ABC中,DA⊥AB,AD=AB,EA⊥AC,AE=AC.
(1)试说明△ACD≌△AEB;
(2)若∠ACB=90°,连接CE,
①说明EC平分∠ACB;
②判断DC与EB的位置关系,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)求证:△OAE≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点,且∠DBC=∠A,连接OE并延长与⊙O相交于点F,与BC相交于点C.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为6,BC=8,求弦BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.

(1)求抛物线的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.

(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
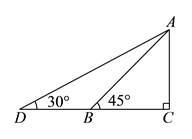
【题目】(![]() 分)如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由
分)如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由![]() 降为
降为![]() ,已知
,已知![]() 米,点
米,点![]() ,
, ![]() ,
, ![]() 在同一水平地面上,
在同一水平地面上, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 在同一平面内.
在同一平面内.
(![]() )求改善后滑滑板
)求改善后滑滑板![]() 的长.
的长.
(![]() )若滑滑板的正前方有
)若滑滑板的正前方有![]() 米长的空地就能保证安全,原滑滑板的前方有
米长的空地就能保证安全,原滑滑板的前方有![]() 米长的空地,这样改善方案是否可行?说明理由.
米长的空地,这样改善方案是否可行?说明理由.
(![]() )∵在
)∵在![]() 中,
中, ![]() ,
,
∴![]() 米.
米.
(或:∵在![]() 中,
中, ![]() ,∴
,∴![]() 米).
米).
答:改善后![]() 长
长![]() 米.
米.
(![]() )∵在
)∵在![]() 中,
中, ![]() ,
,
∴![]() 米,
米,
∵在![]() 中,
中, ![]() ,
,
∴![]() 米,
米,
∴![]() 米,
米,
∵![]() 米,
米, ![]() ,
,
∴这样的改善方案可行.
查看答案和解析>>
科目:初中数学 来源: 题型:
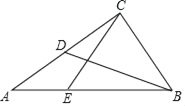
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,BC=![]() ,cot∠ABC=
,cot∠ABC=![]() ,点D是AC的中点.
,点D是AC的中点.
(1)求线段BD的长;
(2)点E在边AB上,且CE=CB,求△ACE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com