
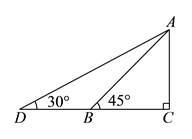
【题目】(![]() 分)如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由
分)如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由![]() 降为
降为![]() ,已知
,已知![]() 米,点
米,点![]() ,
, ![]() ,
, ![]() 在同一水平地面上,
在同一水平地面上, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 在同一平面内.
在同一平面内.
(![]() )求改善后滑滑板
)求改善后滑滑板![]() 的长.
的长.
(![]() )若滑滑板的正前方有
)若滑滑板的正前方有![]() 米长的空地就能保证安全,原滑滑板的前方有
米长的空地就能保证安全,原滑滑板的前方有![]() 米长的空地,这样改善方案是否可行?说明理由.
米长的空地,这样改善方案是否可行?说明理由.
(![]() )∵在
)∵在![]() 中,
中, ![]() ,
,
∴![]() 米.
米.
(或:∵在![]() 中,
中, ![]() ,∴
,∴![]() 米).
米).
答:改善后![]() 长
长![]() 米.
米.
(![]() )∵在
)∵在![]() 中,
中, ![]() ,
,
∴![]() 米,
米,
∵在![]() 中,
中, ![]() ,
,
∴![]() 米,
米,
∴![]() 米,
米,
∵![]() 米,
米, ![]() ,
,
∴这样的改善方案可行.
【答案】(1)10米;(2)可行
【解析】试题分析:(1)求AD长的时候,可在直角△ADC内,根据∠D的度数和AC的长,运用正弦函数求出AD的长.
(2)本题实际要求的是BD的长是否超过4m,如果超过了那么这样修改滑板的坡度就不可行,反之,则可行.就要先求出BD的长,也就是求出CD,BC的长,求CD可在直角△ACD中,根据∠D的度数和AC的长,用正切函数求出CD的长;求BC的长,可在直角△ABC内,根据∠ABC的度数和AC的长,用正切函数求出BC,进而求出BD.
解:(![]() )∵在
)∵在![]() 中,
中, ![]() ,
,
∴![]() 米.
米.
(或:∵在![]() 中,
中, ![]() ,∴
,∴![]() 米).
米).
答:改善后![]() 长
长![]() 米.
米.
(![]() )∵在
)∵在![]() 中,
中, ![]() ,
,
∴![]() 米,
米,
∵在![]() 中,
中, ![]() ,
,
∴![]() 米,
米,
∴![]() 米,
米,
∵![]() 米,
米, ![]() ,
,
∴这样的改善方案可行.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:
【题目】某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元.如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄山位于安徽省南部,是世界文化与自然双重遗产,世界地质公园,国家![]() 级旅游景区,全国文明风景旅游区示范点,中华十大名山,天下第一奇山.
级旅游景区,全国文明风景旅游区示范点,中华十大名山,天下第一奇山.
暑假期间,太和县某学校组织七年级学生到黄山游学,如果租用甲种客车2辆,乙种客车3辆,则可载180人,如果租用甲种客车3辆,乙种客车1辆,则可载165人.
(1)请问甲、乙两种客车每辆分别能载客多少人?
(2)若该学校七年级有303名学生参加这次游学活动,学校计划每辆车安排一名老师,老师也需一个座位.
①现打算同时租甲、乙两种客车共8辆,请帮助学校设计租车方案.
②旅行前,学校的一名老师由于特殊情况,学校只能安排7名老师,为保证所租的每辆车均有一名老师,租车方案调整为:同时租65座、45座和30座的大小三种客车,出发时,所租的三种客车的座位恰好坐满,请问学校的租车方案如何安排?
查看答案和解析>>
科目:初中数学 来源: 题型:
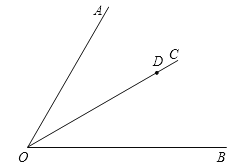
【题目】如图,点D是∠AOB的角平分线OC上的任意一点.
(1)按下列要求画出图形.
①过点D画DE∥OA,DE与OB交于点E;
②过点D画DF⊥OC,垂足为点D,DF与OB交于点F;
③过点D画DG⊥OA,垂足为点G,量得点D到射线OA的距离等于_____mm(精确到1mm);
(2)在(1)所画出的图形中,若∠AOB=n,则∠EDF=____________度(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
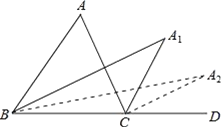
【题目】如图,在△ABC中,∠A=m°,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…∠A2015BC和∠A20l5CD的平分线交于点A2016,则∠A2016=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC直角三角形,延长AB到D,使BD=BC,在BC上取BE=AB,连接DE.△ABC顺时针旋转后能与△EBD重合,那么:
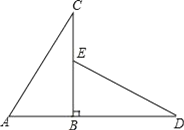
(1)旋转中心是哪一点?旋转角是多少度?
(2)AC与DE的关系怎样?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组在“用频率估计概率”的实验中,统计了某种结果出现的频率,绘制了如图所示的折线图,那么符合这一结果的实验最有可能的是( )
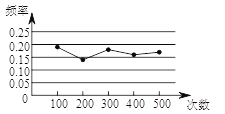
A. 袋子中有1个红球和2个黄球,它们只有颜色上的区别,从中随机地取出一个球是黄球
B. 掷一个质地均匀的正六面体骰子,落地时面朝上的点数是6
C. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
D. 掷一枚质地均匀的硬币,落地时结果是“正面向上”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数 y=-2x+5 的图像分别与 x 轴,y 轴交于点A、B,以线段AB 为边在第一象限内作等腰 RtABC,BAC=90 ,求过 B、C 两点的直线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列证明过程填空,请在括号里面填写对应的推理的理由.如图,已知:直线AB、CD被直线BC所截;直线BC、DE被直线CD所截,∠1+∠2 =180°,且∠1=∠D,求证:BC∥DE.
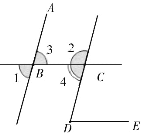
证明:∵∠1+∠2=180°(已知)
又∵∠1=∠3 .
∴∠2+∠3=180°(等量代换)
∴AB∥ .
∴∠4=∠1 .
又∵∠1=∠D .
∴∠D= (等量代换)
∴BC∥DE( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com