【题目】甲、乙、丙三名打字员承担一项打字任务，已知如下信息：
信息一：甲单独完成任务所需时间比乙单独完成任务所需时间多5小时；
信息二：甲4小时完成的工作量与乙3小时完成的工作量相等；
信息三：丙的工作效率是甲的工作效率的2倍．
如果每小时只安排1名打字员，那么按照甲、乙、丙的顺序至完成工作任务，共需（ ）
A.
小时B.
小时C.
小时D.
小时
科目：初中数学 来源： 题型：
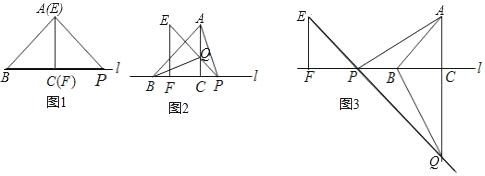
【题目】如图1，△ABC的边BC在直线l上，AC⊥BC，且AC＝BC；△EFP的边FP也在直线l上，边EF与边AC重合，且EF＝FP(备注：当EF＝FP，∠EFP＝90°时，∠PEF＝∠FPE＝45°，反之当∠PEF＝∠FPE＝45°时，当EF＝FP)．
(1)在图1中，请你通过观察、测量、猜想并写出AB与AP所满足的数量关系和位置关系．
(2)将△EFP沿直线l向左平移到图2的位置时，EP交AC于点Q，连接AP，BQ．猜想并写出BQ与AP所满足的数量关系和位置关系，并证明你的猜想；
(3)将△EFP沿直线l向左平移到图3的位置时，EP的延长线交AC的延长线于点Q，连接AP、BQ．你认为(2)中所猜想的BQ与AP的结论还成立吗？若成立，给出证明：若不成立，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知二次函数y＝x2＋mx＋n的图象经过A(0，3)，且对称轴是直线x＝2.
(1)求该函数的解析式；
(2)在抛物线上找一点P，使△PBC的面积是△ABC的面积的
，求出点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一个水槽有进水管和出水管各一个，进水管每分钟进水a升，出水管每分钟出水b升．水槽在开始5分钟内只进水不出水，随后15分钟内既进水又出水，得到时间x(分)与水槽内的水量y(升)之间的函数关系(如图所示)．
(1)求a、b的值；
(2)如果在20分钟之后只出水不进水，求这段时间内y关于x的函数解析式及定义域．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，A、B是双曲线y=
（k＞0）上的点，A、B两点的横坐标分别是a、3a，线段AB的延长线交x轴于点C，若S△AOC=3．则k的值为（ ）
A. 2 B. 1.5 C. 4 D. 6
查看答案和解析>>
科目：初中数学 来源： 题型：
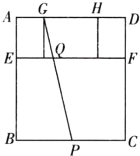
【题目】如图，一个长方形窗框
被
分成上下两个长方形，上部分长方形又被分成三个小长方形，其中
，
为
的四等分点（在左侧）且
．一晾衣杆斜靠在窗框上的
位置，
为
中点．若
，分长方形
的左右面积之比为
，则分长方形
的左右面积之比为________．（用含
，
的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是等腰直角三角形，∠BCA＝90°，BC＝AC，直角顶点C在y轴上，锐角顶点A在x轴上．
（1）如图①，若点C的坐标是（0，﹣1），点A的坐标是（﹣3，0），求B点的坐标；
（2）如图②，若x轴恰好平分∠BAC，BC与x轴交于点D，过点B作BE⊥x轴于E，问AD与BE有怎样的数量关系，并说明理由；
（3）如图③，直角边AC在两坐标轴上滑动，使点B在第四象限内，过B点作BF⊥x轴于F，在滑动的过程中，猜想OC、BF、OA之间的关系，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】根据题意结合图形填空：
已知：如图，AD⊥BC于D，EG⊥BC与G，∠E=∠3，试问：AD是∠BAC的平分线吗？若是，请说明理由．
答：是，理由如下：
∵AD⊥BC，EG⊥BC（___________）
∴∠4=∠5=90°（___________________________）
∴AD∥EG（________________________________）
∴∠1=∠E____________________________）
∠2=∠3（__________________________________）
∵∠E=∠3（________________）
∴________________（ 等量代换 ）
∴AD是∠BAC的平分线（_____________________）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】己知：
为等边三角形，点E为射线AC上一点，点D为射线CB上一点，
．
(1)如图1，当E在AC的延长线上且
时，AD是的中线吗？请说明理由；
(2)如图2，当E在AC的延长线上时，
等于AE吗？请说明理由;
(3)如图3，当D在线段CB的延长线上，E在线段AC上时，请直接写出AB、BD、AE的数量关系．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
