
����Ŀ����ͼ����ABC�ǵ���ֱ�������Σ���BCA��90����BC��AC��ֱ�Ƕ���C��y���ϣ���Ƕ���A��x���ϣ�

��1����ͼ�٣�����C�������ǣ�0����1������A�������ǣ���3��0������B������ꣻ
��2����ͼ�ڣ���x��ǡ��ƽ�֡�BAC��BC��x�ύ�ڵ�D������B��BE��x����E����AD��BE��������������ϵ����˵�����ɣ�
��3����ͼ�ۣ�ֱ�DZ�AC�����������ϻ�����ʹ��B�ڵ��������ڣ���B����BF��x����F���ڻ����Ĺ����У�����OC��BF��OA֮��Ĺ�ϵ����֤����Ľ��ۣ�
���𰸡���1��B��1��2������2��AD��2BE�����ɼ���������3��OC��BF+OA�����ɼ�����
��������
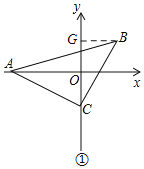
��1������ͼ�٣���B��BG��y����G��֤����AOC�ա�CGB��AAS������AO=CG=3��OC=BG=1����ʾ��B�����ꣻ
��2����ͼ�ڣ��ӳ�BE��AC����H��֤����AEB�ա�AEH��ASA������BE=EH����BH=2BE����֤����ACD�ա�BCH��ASA�����ɵý��ۣ�
��3����ͼ�ۣ���C��CM��BF����FB���ӳ�����M��֤����AOC�ա�BMC��AAS�����ı���OCMFΪ���Σ������߶εĺͿɵý��ۣ�
��1����ͼ�٣���B��BG��y����G��
�ߵ�C�������ǣ�0����1������A�������ǣ���3��0����
��OC��1��OA��3��
�ߡ�BCA��90����
���ACO+��BCG��90����
�ߡ�BCG+��CBG��90����
���ACO����CBG��
��AC��BC����AOC����BGC��90����
���AOC�ա�CGB��AAS����
��AO��CG��3��OC��BG��1��
��OG��3��1��2��
��B��1��2����
��2����ͼ�ڣ�AD��2BE��
�����ǣ��ӳ�BE��AC����H��

��BE��x�ᣬ
���AEB����AEH��90����
��AEƽ�֡�BAC��
���CAD����BAD��
��AE��AE��
���AEB�ա�AEH��ASA����
��BE��EH����BH��2BE��
�ߡ�ACD����BED��90������ADC����BDE��
���CAD����CBH��
��AC��BC����ACD����BCH��90����
���ACD�ա�BCH��ASA����
��AD��BH��2BE��
��3��OC��BF+OA��
�����ǣ���ͼ�ۣ���C��CM��BF����FB���ӳ�����M��

ͬ���ɵã���AOC�ա�BMC��AAS����
��AO��BM��OC��CM��
�ߡ�COF����OFM����M��90����
���ı���OCMFΪ���Σ�
��FM��OC��
��FM��BF+BM��
��OC��BF+OA��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC������A����B����C�ĶԱ߷ֱ��Ϊ![]() ��
��![]() ��
��![]() �����������������ж���ABCΪֱ�������ε����� ����
�����������������ж���ABCΪֱ�������ε����� ����
A����A+��B=��C
B����A�á�B�á�C =1��2��3
C��![]()
D��![]() ��
��![]() ��
��![]() =3��4��6
=3��4��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��x���ʾһ����������ĵ�·��y���ʾһ���ϱ�����ĵ�·��С����С���ֱ��ʮ��·��O�㴦ͬʱ������С������x����4ǧ��ʱ���ٶ�������ǰ����С������y����5ǧ��/ʱ���ٶ�������ǰ������һ�Ű������λ��ͼ�е�P�㴦��������x�ᡢy��ľ���ֱ���3ǧ��2ǧ�ף�
�ʣ���1���뿪·�ں�����ʱ�䣬��������ù����ľ���ǡ����ȣ�
��2���뿪·�ھ�������ʱ�䣬��������Ź���������λ��ǡ����һ��ֱ���ϣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ�����������Ա�е�һ�����������֪������Ϣ��
��Ϣһ�����������������ʱ����ҵ��������������ʱ���5Сʱ��
��Ϣ������4Сʱ��ɵĹ���������3Сʱ��ɵĹ�������ȣ�
��Ϣ�������Ĺ���Ч���ǼĹ���Ч�ʵ�2����
���ÿСʱֻ����1������Ա����ô���ռס��ҡ�����˳������ɹ��������裨 ��
A.![]() СʱB.
СʱB.![]() СʱC.
СʱC.![]() СʱD.
СʱD.![]() Сʱ
Сʱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�EΪBC����һ�㣬����AE����֪AB=8��CE=2��F���߶�AE��һ���㣮��BF���ӳ��߽�������ABCD��һ���ڵ�G��������AE=BG����![]() ��ֵΪ________��
��ֵΪ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������˶�Ա��������������һ���Ƕȵķ����߳���������е�·����һ�������ߣ������ǿ�������������������ĸ߶�![]() ����λ��
����λ��![]() ���������߳�����ʱ��
���������߳�����ʱ��![]() ����λ��
����λ��![]() ��֮��Ĺ�ϵ���±���
��֮��Ĺ�ϵ���±���
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | �� |
| 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | �� |
���н��ۣ�����������������߶�Ϊ![]() �����������·�ߵĶԳ�����ֱ��
�����������·�ߵĶԳ�����ֱ��![]() ���������߳�
���������߳�![]() ʱ��أ��������߳�
ʱ��أ��������߳�![]() ʱ���������ĸ߶���
ʱ���������ĸ߶���![]() .
.
������ȷ���۵ĸ����ǣ� ��
A��1 B��2 C��3 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����P�ǡ�AOB�ڲ���һ�㣬��Ҫ��������и�С��.
(1)�ֱ���P����OA��OB�ĶԳƵ�ֱ�ΪP1��P2������P1P2, �ֱ�OA��OB�ڵ�M��N����.
(2)����PM��PN����P1P2=5cm������PMN���ܳ�= cm;
(3)������OP1��OP2������AOB=55�������P1OP2= ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC �У���ABC=63������ D��E �ֱ��ǡ�ABC �ı�BC��AC �ϵĵ㣬�� AB=AD=DE=EC�����C �Ķ����ǣ� ��

A.21��B.19��C.18��D.17��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AOB�ǵȱ������Σ�AB=4����ABCD�������
��2����ͼ2������ABC�У���B=90�㣬��A=30�㣬D�DZ�AB��һ�㣬��BDC=45�㣬AD=4����BC�ij�������������ţ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com