
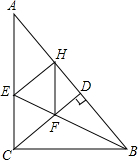
 已知,如图,△ABC中,∠ACB=90°,BE平分∠ABC,CD⊥AB于D,EH⊥B于H,CD交BE于F,求证:四边形CEHF为菱形.
已知,如图,△ABC中,∠ACB=90°,BE平分∠ABC,CD⊥AB于D,EH⊥B于H,CD交BE于F,求证:四边形CEHF为菱形. 分析 根据角平分线性质求出CE=EH,求出CE=CF,推出EH∥CF,EH=CF,得出平行四边形CEHF,根据菱形的判定推出即可.
解答 证明:∵BE平分∠CBA,
∴∠CBE=∠HBE,
∵∠ACB=90°,CD⊥AB,
∴∠ACB=∠BDF,
∵∠EFC=∠DFB=90°-∠HBE,∠CEF=90°-∠CBE,
∴∠CEF=∠CFE,
∴CE=CF,
∵BE平分∠CBA,∠ACB=90°,EH⊥AB,
∴CE=EH,
∴CF=EH,
∵EH⊥AB,CD⊥AB,
∴CF∥EH,
∵CF=EH,CF=CE,
∴四边形CEHF是菱形.
点评 本题考查了平行四边形的判定,菱形的判定,角平分线性质,等腰三角形的判定的应用,解此题的关键是推出CF=EH,题目综合性比较强,有一定的难度.


科目:初中数学 来源: 题型:填空题
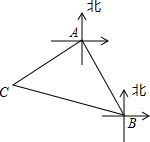 如图,已知小岛B在基地A的南偏东30°方向上,与基地A相距10海里,货轮C在基地A的南偏西60°方向、小岛B的北偏西75°方向上,那么货轮C与小岛B的距离是10$\sqrt{2}$海里.
如图,已知小岛B在基地A的南偏东30°方向上,与基地A相距10海里,货轮C在基地A的南偏西60°方向、小岛B的北偏西75°方向上,那么货轮C与小岛B的距离是10$\sqrt{2}$海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 下降高度d(米) | 20 | 80 | 245 | 320 |
| 下降时间t(秒) | 2 | 4 | 7 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
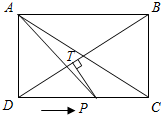 如图,在矩形ABCD中,AD=60cm,CD=80cm,连接AC、BD.动点P从点D出发,以5cm/s速度沿边DC匀速向点C运动,到达点C即停止,过点P作BD的垂线,垂足为T.设点P运动的时间为t s.
如图,在矩形ABCD中,AD=60cm,CD=80cm,连接AC、BD.动点P从点D出发,以5cm/s速度沿边DC匀速向点C运动,到达点C即停止,过点P作BD的垂线,垂足为T.设点P运动的时间为t s.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com