
���� ��1����2012��2014�����ƽ��������Ϊx���õ�3000��1+x��2=3630�����x��Ȼ�����3630��1+x���õ�2015����¹��ʣ�
��2����������鵥��ΪmԪ����һ��ѡ��y�������ҹ����鵥��ΪnԪ����һ��ѡ��z�������ݵ�����ϵ����363Ԫ�����˼ס������ֹ������һ����ʵ�ʸ����2015��6�·ݵ��¹�������363Ԫ��2015��6�·ݵ��¹��ʸպù������ɱ����ֹ������һЩ���ֹ����飮�г���������⼴�ɣ�
��� �⣺��1����2012��2014�����ƽ��������Ϊx���������з��̣�
3000��1+x��2=3630��
��ã�x1=10%��x2=-210%��
�������ʲ����Ǹ�����
��-210%Ҫ��ȥ��
��ǿ2015����¹���Ϊ��3630��1+10%��=3993Ԫ��
����ǿ2015����¹���Ϊ3993Ԫ��
��2��������鵥��ΪmԪ����һ��ѡ��y�������ҹ����鵥��ΪnԪ����һ��ѡ��z�����������⣬���з��̣�
$\left\{\begin{array}{l}{m+n=363��}\\{ny+mz=3993��}\\{my+nz=3993-363��}\end{array}\right.$��
�ɢ�+�ۣ������ã���m+n����y+z��=2��3993-363��
�Ѣٴ���ã�363��y+z��=2��3993-363��
��y+z=22-1=21��
21+2=23����
����ǿ�ܹ�������23�������飮
���� ���⿼�����һԪ���η��̵�Ӧ�ã�ע����������ϵ��������˼�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
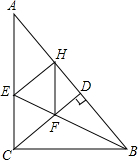 ��֪����ͼ����ABC�У���ACB=90�㣬BEƽ�֡�ABC��CD��AB��D��EH��B��H��CD��BE��F����֤���ı���CEHFΪ���Σ�
��֪����ͼ����ABC�У���ACB=90�㣬BEƽ�֡�ABC��CD��AB��D��EH��B��H��CD��BE��F����֤���ı���CEHFΪ���Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
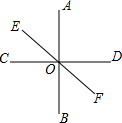 ��ͼ��ʾ��ֱ��AB��CD��EF�ཻ�ڵ�O��AB��CD����AOE=$\frac{1}{2}$��AOD�����BOF���BOE�Ķ�����
��ͼ��ʾ��ֱ��AB��CD��EF�ཻ�ڵ�O��AB��CD����AOE=$\frac{1}{2}$��AOD�����BOF���BOE�Ķ������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com