
【题目】已知:如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]()

(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当![]() 取何值时,反比例函数的值大于正比例函数的值?
取何值时,反比例函数的值大于正比例函数的值?
(3)![]() 是反比例函数图象上的一动点,其中
是反比例函数图象上的一动点,其中![]() 过点
过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ;过点
;过点![]() 作直线
作直线![]() 轴交
轴交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .当四边形
.当四边形![]() 的面积为6时,请判断线段
的面积为6时,请判断线段![]() 与
与![]() 的大小关系,并说明理由.
的大小关系,并说明理由.
【答案】(1)反比例函数的表达式为:![]()
正比例函数的表达式为![]()
(2)第一象限内,当![]() 时,反比例函数的值大于正比例函数的值.
时,反比例函数的值大于正比例函数的值.
(3)![]() ,理由见解析
,理由见解析
【解析】
(1)将A(3,2)分别代入y=![]() ,y=ax中,得ak的值,进而可得正比例函数和反比例函数的表达式;
,y=ax中,得ak的值,进而可得正比例函数和反比例函数的表达式;
(2)观察图象,得在第一象限内,当0<x<3时,反比例函数的图象在正比例函数的上方;故反比例函数的值大于正比例函数的值;
(3)有S△OMB=S△OAC=![]() ×|k|=3,可得S矩形OBDC为12;即OCOB=12;进而可得mn的值,故可得BM与DM的大小;比较可得其大小关系.
×|k|=3,可得S矩形OBDC为12;即OCOB=12;进而可得mn的值,故可得BM与DM的大小;比较可得其大小关系.
解:(1)将![]() 分别代入
分别代入![]() 中,得
中,得![]()
∴![]()
∴反比例函数的表达式为:![]()
正比例函数的表达式为![]()
(2)第一象限内,当![]() 时,反比例函数的值大于正比例函数的值.
时,反比例函数的值大于正比例函数的值.
(3)![]()
理由:∵![]()
∴![]() 即
即![]()
∵![]() ∴
∴![]()
即![]() ∴
∴![]() ∴
∴![]() ∴
∴![]()


科目:初中数学 来源: 题型:
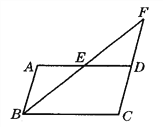
【题目】如图,平行四边形ABCD中,点E是AD的中点,BE的延长线与CD的延长线交于点F.
(1)求证:△ABE≌△DFE;
(2)试连结BD,AF,判断四边形ABDF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小军两同学做游戏,游戏规则是:一个不透明的文具袋中,装有型号完全相同的3个红球和2个黑球,两人先后从袋中取出一个球(不放回),若两人所取球的颜色相同,则小明胜;否则,小军胜;
(1)请用树状图法求出摸笔游戏所有可能的结果;
(2)计算小明获胜的概率是 ,小军获胜的概率是 ,并指出本游戏规则是否公平,若不公平,你认为对谁有利.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座抛物线型拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m, 就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,![]() 的顶点均在格点上,
的顶点均在格点上,![]() ,
,![]() 也在格点上.
也在格点上.

(1)画出![]() 先向右平移5个单位长度,再向下平移5个单位长度得到的
先向右平移5个单位长度,再向下平移5个单位长度得到的![]() ;
;
(2)画出![]() 关于直线
关于直线![]() 对称的
对称的![]() ;
;
(3)画出![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 后所得的
后所得的![]() ;
;
(4)![]() 与
与![]() 组成的图形是轴对称图形吗?如果是轴对称图形,请画出对称轴.
组成的图形是轴对称图形吗?如果是轴对称图形,请画出对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).
根据图象提供的信息,解答下列问题:

(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达到30万元;
(3)求第8个月公司所获利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x+![]() )2+k(a>0),点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)是图象上的三个点,则y1、y2、y3的大小关系是_____(用“<”连接).
)2+k(a>0),点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)是图象上的三个点,则y1、y2、y3的大小关系是_____(用“<”连接).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com