
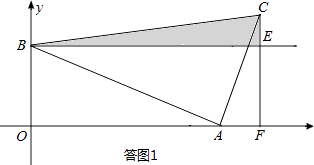
����Ŀ����ͼ1����A��x���������ϵĶ��㣬��B����Ϊ��0��4����M���߶�AB���е㣬����M�Ƶ�A˳ʱ�뷽����ת90��õ���C������C��x��Ĵ��ߣ�����ΪF������B��y��Ĵ�����ֱ��CF�ཻ�ڵ�E����D�ǵ�A����ֱ��CF�ĶԳƵ㣬����AC��BC��CD�����A�ĺ�����Ϊt��
��1����t=2ʱ����CF�ij���
��2���ٵ�tΪ��ֵʱ����C�����߶�BD�ϣ�
�����BCE�����ΪS����S��t֮��ĺ�����ϵʽ��
��3����ͼ2������C���E�غ�ʱ������CDF��x������ƽ�Ƶõ���C��D��F�䣬�ٽ�A��B��C�䣬D��Ϊ������ı�����C��F��������õ�����ͼ�Σ���������ͼ��ƴ�ɲ��ص�����϶��ͼ��ǡ���������Σ���ֱ��д�����з������������ĵ�C������꣮
���𰸡�
��1��
�⣺�����⣬��֤Rt��ACF��Rt��BAO��
�� ![]() ��
��
��AB=2AM=2AC��
��CF= ![]() OA=
OA= ![]() t��
t��
��t=2ʱ��CF=1
��2��
�⣺���ɣ�1��֪��Rt��ACF��Rt��BAO��
�� ![]() ��
��
��AF= ![]() OB=2��
OB=2��
��FD=AF=2����
�ߵ�C�����߶�BD�ϣ�
���DCF�ס�DBO��
�� ![]() ����
���� ![]() ��
��
���t= ![]() ��2��t=��
��2��t=�� ![]() ��2��С��0����ȥ��
��2��С��0����ȥ��
�൱t= ![]() ��2ʱ����C�����߶�BD�ϣ�
��2ʱ����C�����߶�BD�ϣ�
�ڵ�0��t��8ʱ������ͼ1��ʾ��
S= ![]() BECE=
BECE= ![]() ��t+2����4��
��t+2����4�� ![]() t��=-
t��=- ![]() t2+
t2+ ![]() t+4��
t+4��
��t��8ʱ�����ͼ1��ʾ��
S= ![]() BECE=
BECE= ![]() ��t+2����
��t+2���� ![]() t��4��=
t��4��= ![]() t2��
t2�� ![]() t��4
t��4
��3��
�⣺���������ĵ�C������Ϊ����12��4������8��4����2��4����
�������£�
�ڡ�CDF��x������ƽ�ƵĹ����У����������ļ�ƴ���������֣�
����һ�����ͼ2��ʾ����F��C��=AF��ʱ����F�������Ϊ��12��0����
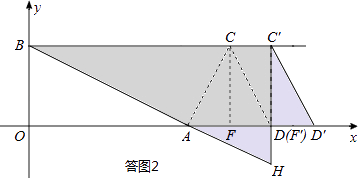
���ݡ�C��D��F��ա�AHF�䣬��BC��HΪƴ�ɵ������Σ���ʱC�������Ϊ��12��4����
�����������ͼ3��ʾ������F�����A�غ�ʱ����F�������Ϊ��8��0����

���ݡ�OC��A�ա�BAC�䣬��֪��OC��D��Ϊƴ�ɵ������Σ���ʱC�������Ϊ��8��4����
����������BC��=F��D��ʱ����F�������Ϊ��2��0����
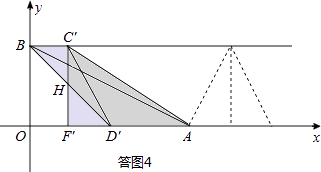
���ݡ�BC��H�ա�D��F��H����֪��AF��C��Ϊƴ�ɵ������Σ���ʱC�������Ϊ��2��4��
����������1����Rt��ACF��Rt��BAO����CF= ![]() OA=
OA= ![]() t���ɴ����CF��ֵ����2������Rt��ACF��Rt��BAO���������AF�ij��ȣ�����C�����߶�BD�ϣ����С�DCF�ס�DBO���������Ʊ���ʽ�з������t��ֵ��
t���ɴ����CF��ֵ����2������Rt��ACF��Rt��BAO���������AF�ij��ȣ�����C�����߶�BD�ϣ����С�DCF�ס�DBO���������Ʊ���ʽ�з������t��ֵ��
���������������Ҫ�������ۣ���0��t��8ʱ������ͼ1��ʾ����t��8ʱ�����ͼ1��ʾ����3�������漰ͼ�εļ�ƴ���ڡ�CDF��x������ƽ�ƵĹ����У����������ļ�ƴ���������֣���Ҫ�������ۣ��ֱ����ͼ2��4��ʾ��
�����㾫����������Ҫ����������ͼ�κ����������ε��ж������ʵ����֪ʶ�㣬��Ҫ������״��ͬ����С��һ����ͬ���Ŵ����С��;�ж�:��ƽ�У���������ȣ������߶�Ӧ�ɱ������н���ȣ������߶�Ӧ�ɱ��������������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ��������ȷ�����⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺����Ʒ���Ӽ�40%��Ϊ���ۼۣ�Ԫ���ڼ���Żݴ����������ɹ˿ͳ齱ȷ���ۿۣ�ij�˿���ס���������Ʒ���ֱ�鵽���ۺ;��ۣ�������399Ԫ���̳���ӯ��49Ԫ���ס���������Ʒ�Ľ��۷ֱ�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֱ��������ABC����A��x���ϣ���BCA=90�㣬AC=BC=2 ![]() ������������y=
������������y= ![]() ��x��0����ͼ��ֱ���AB��BC���ڵ�D��E������DE������BDE�ס�BCAʱ����E������Ϊ ��
��x��0����ͼ��ֱ���AB��BC���ڵ�D��E������DE������BDE�ס�BCAʱ����E������Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P�Ƿ���������y= ![]() ��k��0��ͼ���ϵĵ㣬PA��ֱx���ڵ�A����1��0������C������Ϊ��1��0����PC��y���ڵ�B������AB����֪AB=
��k��0��ͼ���ϵĵ㣬PA��ֱx���ڵ�A����1��0������C������Ϊ��1��0����PC��y���ڵ�B������AB����֪AB= ![]() ��
��
��1��k��ֵ����
��2����M��a��b���Ǹ÷���������ͼ���ϵĵ㣬�������MBA����ABC����a��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB��CD�Ĺ�������BD=![]() AB=
AB= ![]() CD���߶�AB��CD���е�E��F֮�������10cm����AB��CD�ij���
CD���߶�AB��CD���е�E��F֮�������10cm����AB��CD�ij���
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�����������ֱ��Ϊ7cm��Բ���ι�ͷ�У��轫��Ģ����ͷ���������ڹ�ͷ���森Ϊ�˻�ýϼ��Ӿ�Ч���������ڹ�ͷ�в������γɵĻ��Ķ���Ϊ90�㣬��Ģ����ͷ�������ij���Ϊ�� �� 
A.![]() cm
cm
B.![]() cm
cm
C.![]() cm
cm
D.7��cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����
��Ҫ�˽�һ�����ݵ�ʹ��������Ӧ�����ղ�ķ�ʽ��
����һ����Ϸ���н�����1%������100����������Ϸһ�����н���
�ۼס����������ݵ�����������ƽ�����ֱ���ͬ�������� ![]() =0.1��
=0.1�� ![]() =0.2����������ݱ����������ȶ���
=0.2����������ݱ����������ȶ���
�ܡ���һöӲ�ң����泯�ϡ��DZ�Ȼ�¼���
��ȷ˵��������ǣ� ��
A.��
B.��
C.��
D.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+1��k��0���뷴��������y= ![]() ��m��0����ͼ���й�����A��1��2����ֱ��l��x���ڵ�N��3��0������һ�κ����ͷ�����������ͼ��ֱ��ڵ�B��C��
��m��0����ͼ���й�����A��1��2����ֱ��l��x���ڵ�N��3��0������һ�κ����ͷ�����������ͼ��ֱ��ڵ�B��C�� 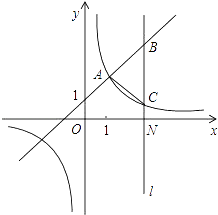
��1����һ�κ����뷴���������Ľ���ʽ��
��2�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AD=10��AB=4����Q��BC���е㣬��P��AD�����˶�������BPQ�ǵ���������ʱ��AP�ij�Ϊ .

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com