
 如图,四边形ABCD内接于圆,延长AD、BC相交于点E,点F是BD的延长线上的点,且AB=AC.
如图,四边形ABCD内接于圆,延长AD、BC相交于点E,点F是BD的延长线上的点,且AB=AC.分析 (1)由∠ABC+∠ADC=180°,∠CDE+∠ADC=180°,推出∠CDE=∠ABC,由∠EDF=∠ADB=∠ACB,以及AB=AC,推出∠ABC=∠ACB,即可推出∠EDF=∠CDE解决问题.
(2)证△ABD∽△AEB,通过相似三角形的对应成比例线段,求出DE的值.
解答 (1)证明:∵∠ABC+∠ADC=180°,∠CDE+∠ADC=180°,
∴∠CDE=∠ABC,
∵∠EDF=∠ADB=∠ACB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠EDF=∠CDE,
∴DE平分∠CDF.
(2)解:∵∠ADB=∠ABC,∠DAB=∠BAE,
∴△ABD∽△AEB
∴$\frac{AB}{AE}$=$\frac{AD}{AB}$,
∵AB=AC=3,AD=2
∴AE=$\frac{A{B}^{2}}{AD}$=$\frac{9}{2}$,
∴DE=$\frac{9}{2}$-2=$\frac{5}{2}$(cm).
点评 本题综合考查了角平分线的判定,相似三角形的判定和性质,圆内接四边形的性质等知识,解题的关键是灵活运用所学知识,学会正确寻找相似三角形解决问题,属于中考常考题型..


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
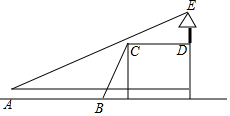 如图,小周站在A处,他的对面有一斜坡BC(坡度i=12:5),现测得小周所站A处到斜坡底端B的距离,AB=15米,坡面BC长为13米.在斜坡顶端C不远处D有一棵树,测得CD=10米,小周看树的顶部E的仰角为30°,此时小周眼睛到地面的高度为1.8米,则数的高度DE约为( )(精确到1米,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24)
如图,小周站在A处,他的对面有一斜坡BC(坡度i=12:5),现测得小周所站A处到斜坡底端B的距离,AB=15米,坡面BC长为13米.在斜坡顶端C不远处D有一棵树,测得CD=10米,小周看树的顶部E的仰角为30°,此时小周眼睛到地面的高度为1.8米,则数的高度DE约为( )(精确到1米,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24)| A. | 5 | B. | 7 | C. | 12 | D. | 17 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
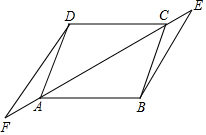 如图,?ABCD中,E,F是直线AC上两点,请在题目中添加合适的条件,就可以证明:BE=DF.
如图,?ABCD中,E,F是直线AC上两点,请在题目中添加合适的条件,就可以证明:BE=DF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
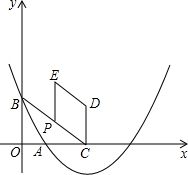 如图在平面直角坐标系xOy中,抛物线y=$\frac{\sqrt{3}}{5}{x}^{2}$+bx+c过点A(1,0),B(0,$\sqrt{3}$),这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),射线PC绕点P逆时针旋转120°,得线段PE,作平行四边形PCDE.
如图在平面直角坐标系xOy中,抛物线y=$\frac{\sqrt{3}}{5}{x}^{2}$+bx+c过点A(1,0),B(0,$\sqrt{3}$),这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),射线PC绕点P逆时针旋转120°,得线段PE,作平行四边形PCDE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com