
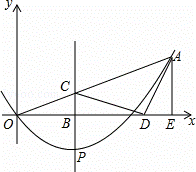
如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x=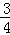 ,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.
,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.
(1)求抛物线的解析式;
(2)填空:
①用含m的式子表示点C,D的坐标:
C( , ),D( , );
②当m= 1 时,△ACD的周长最小;
(3)若△ACD为等腰三角形,求出所有符合条件的点P的坐标.
解:(1)依题意,得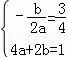 ,解得
,解得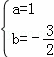
∴y=x2﹣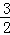 x
x
(2)C(m,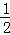 m),D(2m,0),m=1
m),D(2m,0),m=1
(3)依题意,得B(m,0)
在RT△OBC中,OC2=OB2+BC2=m2+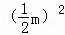 =
=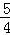 m2,
m2,
∴OC=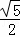 m 又∵O,D关于直线PC对称,
m 又∵O,D关于直线PC对称,
∴CD=OC=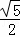 m
m
在RT△AOE中,OA=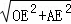 =
=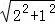 =
=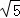
∴AC=OA﹣OC=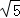 ﹣
﹣ m
m
在RT△ADE中,AD2=AE 2+DE2=12+(2﹣2m)2=4m2﹣8m+5
2+DE2=12+(2﹣2m)2=4m2﹣8m+5
分三种情况讨论:
①若AC=CD,即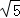 ﹣
﹣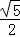 m=
m=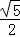 m,解得m=1,∴P(1,
m,解得m=1,∴P(1, )
)
②若AC=AD,则有AC2=AD2,即5﹣5m+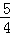 m2=4m2﹣8m+5
m2=4m2﹣8m+5
解得m1=0,m2=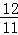 .∵0<m<2,∴m=
.∵0<m<2,∴m=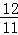 ,∴P(
,∴P(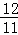 ,
,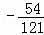 )
)
③若DA=DC,则有D A2=DC2,即4m2﹣8m+5=
A2=DC2,即4m2﹣8m+5= m2
m2
解得m1=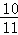 ,m2=2,∵,0<m<2,∴m=
,m2=2,∵,0<m<2,∴m=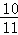 ,∴P(
,∴P(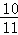 ,
,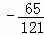 )
)
综上所述,当△ACD为等腰三角形是,点P的坐标分别为P1(1,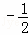 ),P2(
),P2(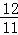 ,
,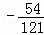 ),P3(
),P3(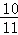 ,
,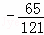 ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
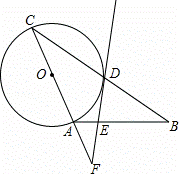
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6,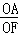 =
=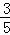 时,求DE的长.
时,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com