
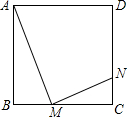
 正方形ABCD边长为4,M、N分别是BC、CD上两个动点,当M点在BC上运动时,始终保持AM和MN垂直.
正方形ABCD边长为4,M、N分别是BC、CD上两个动点,当M点在BC上运动时,始终保持AM和MN垂直.分析 (1)根据正方形的性质得∠B=∠C=90°,∠AMB+∠BAM=90°,又∠AMN=90°,则∠AMB+∠NMC=90°,得到∠BAM=∠NMC,根据相似三角形的判定得到Rt△ABM∽Rt△MCN,由正方形的边长为4,BM=x,由BC-BM表示出MC,再由第一问得到的两三角形相似,根据相似三角形对应边成比例列出关系式,将AB,BM及MC代入,表示出NC,由NC与AB平行不相等,且角B为直角,可得出ABCN为直角梯形,根据梯形的面积公式表示出梯形的面积,可得出y与x的函数关系式;
(2)由于△ABM∽△MCN,那么AB:BM=CM:CN,可求CN,结合四边形ABCN的面积等于9,可得关于x的方程,解即可;
解答 解:(1)∵四边形ABCD为正方形,
∴∠B=∠C=90°,
又∵AM⊥MN,
∴∠AMN=90°,
∴∠AMB+∠NMC=90°,
而∠AMB+∠BAM=90°,
∴∠BAM=∠NMC,
∴Rt△ABM∽Rt△MCN,
∴AB:MC=BM:NC,
而AB=4,BM=x,MC=4-x,
∴4:(4-x)=x:NC,
∴NC=$\frac{4x-{x}^{2}}{4}$,
∴y=$\frac{1}{2}$(NC+AB)•BC
=$\frac{1}{2}$($\frac{4x-{x}^{2}}{4}$+4)×4
=-$\frac{1}{2}$x2+2x+8;
(2)∵△ABM∽△MCN,
∴AB:BM=CM:CN,
∴CN=$\frac{x(4-x)}{4}$,
∴S四边形ABCN=$\frac{1}{2}$×(4+$\frac{x(4-x)}{4}$)×4=9,
解得x1=2+$\sqrt{2}$,x2=2-$\sqrt{2}$,
∴BM=2+$\sqrt{2}$或BM=2-$\sqrt{2}$时,四边形ABCN的面积等于9.
点评 此题考查了相似三角形的判定与性质,正方形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 点P在⊙O内 | B. | 点P在⊙O上 | C. | 点P在⊙O外 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 33=17-(-16) | B. | 65=33-(-32) | C. | 129=65-(-64) | D. | 55=28-(-27) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com