
【题目】如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.
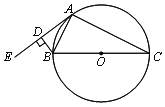
(1)求证:∠DBA=∠ABC;
(2)如果BD=1,tan∠BAD=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题(1)如图,连接OA,由AE为⊙O的切线,BD⊥AE得到∠DAO=∠EDB=90°,于是得到DB∥AO,推出∠DBA=∠BAO,由于OA=OB,得到∠ABC=∠BAO,即可得到结论;
(2)根据三角函数的知识可求出AD,从而根据勾股定理求出AB的长,根据三角函数的知识即可得出⊙O的半径.
试题解析:(1)如图,连接OA,
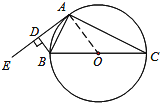
∵AE为⊙O的切线,BD⊥AE,
∴∠DAO=∠EDB=90°,
∴DB∥AO,
∴∠DBA=∠BAO,
又∵OA=OB,
∴∠ABC=∠BAO,
∴∠DBA=∠ABC;
(2)∵BD=1,tan∠BAD=![]() ,
,
∴AD=2,
∴AB=![]() ,
,
∴cos∠DBA=![]() ;
;
∵∠DBA=∠CBA,
∴BC=![]() .
.
∴⊙O的半径为2.5.


科目:初中数学 来源: 题型:
【题目】综合与探究
如图1,抛物线y=ax2+bx+2与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C,连接AC,BC.D为坐标平面第四象限内一点,且使得△ABD与△ABC全等.
(1)求抛物线的表达式.
(2)请直接写出点D的坐标,并判断四边形ACBD的形状.
(3)如图2,将△ABD沿y轴的正方形以每秒1个单位长度的速度平移,得到△A′B′D′,A′B′与BC交于点E,A′D′与AB交于点F.连接EF,AB′,EF与AB′交于点G.设运动的时间为t(0≤t≤2)秒.
①当直线EF经过抛物线的顶点T时,请求出此时t的值;
②请直接写出点G经过的路径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数 y kx b 的图象与 x 轴交点为 A3, 0,与 y 轴交点为 B ,且与正比例函数![]() 的图象交于点C(m,4).
的图象交于点C(m,4).
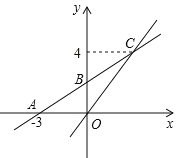
(1)求点C 的坐标;
(2)求一次函数 y kx b 的表达式;
(3)若点 P 是 y 轴上一点,且BPC 的面积为 6,请直接写出点 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=AC=6,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)求点O到直线DE的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,射线AP在△ABC的外侧,点B关于AP的对称点为D,连接CD交射线AP于点E,连接BE.
(1)根据题意补全图形;
(2)求证:CD=EB+EC;
(3)求证:∠ABE=∠ACE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D. 掷一个质地均匀的正六面体骰子,向上的面点数是4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动中,黑板上画着如图所示的图形,活动前老师在准备的四张纸片上分别写有如下四个等式中的一个等式:
①AB=DC,②∠ABE=∠DCE, ③AE=DE,④∠A=∠D.
小明同学闭上眼睛从四张纸片中随机抽取一张,再从剩下的纸片中随机抽取另一张.请结合图形解答下列两个问题:
(1)当抽得①和②时,用①,②作为条件能判定△BEC是等腰三角形吗?说说你的理由;
(2)请你用树状图或表格表示抽取两张纸片上的等式所有可能出现的结果(用序号表示),并求以已经抽取的两张纸片上的等式为条件,使△BEC不能构成等腰三角形的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)过点A(1,﹣3)、B(3,﹣3)、C(﹣1,5),顶点为M点.在抛物线上是找一点P使∠POM=90°,则P点的坐标_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点G,过点G作EF∥BC交AB于E,交AC于F,过点G作GD⊥AC于D,下列四个结论:① EF=BE+CF;②∠BGC=90°+![]() ∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,则
∠A;③点G到△ABC各边的距离相等;④设GD=m,AE+AF=n,则![]() =mn. 其中正确的结论有( )
=mn. 其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com