
【题目】综合与探究
如图1,抛物线y=ax2+bx+2与x轴交于A(﹣1,0),B(4,0)两点,与y轴交于点C,连接AC,BC.D为坐标平面第四象限内一点,且使得△ABD与△ABC全等.
(1)求抛物线的表达式.
(2)请直接写出点D的坐标,并判断四边形ACBD的形状.
(3)如图2,将△ABD沿y轴的正方形以每秒1个单位长度的速度平移,得到△A′B′D′,A′B′与BC交于点E,A′D′与AB交于点F.连接EF,AB′,EF与AB′交于点G.设运动的时间为t(0≤t≤2)秒.
①当直线EF经过抛物线的顶点T时,请求出此时t的值;
②请直接写出点G经过的路径的长.

【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)D(3,﹣2).四边形ACBD是矩形,理由见解析;(3)①t的值为
x+2;(2)D(3,﹣2).四边形ACBD是矩形,理由见解析;(3)①t的值为![]() ;②点G经过的路径的长为1.
;②点G经过的路径的长为1.
【解析】
(1)将A点和B点坐标代入y=ax2+bx+2得a、b的方程组,解此方程组即可得答案,
(2)先利用勾股定理的逆定理证明△ACB为直角三角形,∠ACB=90°,根据△ABD与△ABC全等可知AC=BD,BC=AD,则可证明四边形ABCD为矩形;过点D作DM⊥x轴于M,通过证明△COB≌△DMA,即可求出D点坐标,
(3)①利用二次函数的性质得到顶点T的坐标为(![]() );可得直线BC的解析式为y=﹣
);可得直线BC的解析式为y=﹣![]() x+2,直线AD的解析式为y= -
x+2,直线AD的解析式为y= -![]() x﹣
x﹣![]() ,利用直线的平移得到直线A′D′的解析式为y=﹣
,利用直线的平移得到直线A′D′的解析式为y=﹣![]() x﹣
x﹣![]() +t,直线A′B′的解析式为y=t,则F(2t﹣1,0),E(4﹣2t,t),接着利用待定系数法求出直线EF的解析式为y=
+t,直线A′B′的解析式为y=t,则F(2t﹣1,0),E(4﹣2t,t),接着利用待定系数法求出直线EF的解析式为y=![]() ,然后把T点坐标代入得到关于t的方程,然后解此方程即可;
,然后把T点坐标代入得到关于t的方程,然后解此方程即可;
②先求出直线AB′的解析式为y=![]() ,再解方程组
,再解方程组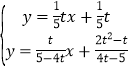 得G(
得G(![]() ),利用G点的坐标特征可判断点G在直线x=
),利用G点的坐标特征可判断点G在直线x=![]() ,然后利用0≤t≤2得到点G经过的路径的长
,然后利用0≤t≤2得到点G经过的路径的长
(1)将A(﹣1,0),B(4,0)两点坐标代入y=ax2+bx+2得![]() ,解得
,解得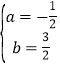 ,
,
∴抛物线的表达式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)D(3,﹣2).四边形ACBD是矩形,理由如下:
当x=0时,得y=2,
∴OC=2,由A(﹣1,0),B(4,0)得OA=1,OB=4.
∴AC2=12+22=5,BC2=22+42=20,AB2=52=25,
∴AC2+BC2=AB2,
∴△ACB为直角三角形,∠ACB=90°,
∵△ABD与△ABC全等,
∴AC=BD,BC=AD,
∴四边形ABCD为平行四边形,
而∠ACB=90°,
∴四边形ABCD为矩形.
如图,过点D作DM⊥x轴于M,
∵∠COB=∠AMD=90°,∠CBA=∠DAB,BC=AD,
∴△COB≌△DMA,
∴AM=OB,OC=DM=2,
∴OM=AM-1=OB-1=3
∴D(3,-2)

(3)①∵y=﹣![]() x2+
x2+![]() x+2=﹣
x+2=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∴顶点T的坐标为(![]() );
);
∵B(4,0) , C(0,2), A(-1,0) D(3,-2)
∴直线BC的解析式为y=﹣![]() x+2,直线AD的解析式为y=﹣
x+2,直线AD的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
∵直线AD向上平移t个单位得到A′D′,直线AB向上平移t个单位得到A′B′,
∴直线A′D′的解析式为y=﹣![]() x﹣
x﹣![]() +t,直线A′B′的解析式为y=t,
+t,直线A′B′的解析式为y=t,
当y=0时,﹣![]() x﹣
x﹣![]() +t=0,解得x=2t﹣1,则F(2t﹣1,0),
+t=0,解得x=2t﹣1,则F(2t﹣1,0),
当y=t时,﹣![]() x+2=t,解得x=4﹣2t,则E(4﹣2t,t),
x+2=t,解得x=4﹣2t,则E(4﹣2t,t),
设直线EF的解析式为y=mx+n,
把E(4﹣2t,t),F(2t﹣1,0)代入得![]() ,解得
,解得 ,
,
∴直线EF的解析式为y=![]() ,
,
把T(![]() )代入得
)代入得![]() ,
,
整理得16t2﹣120t+125=0,解得t1=![]() ,t2=
,t2=![]() (舍去),
(舍去),
∴此时t的值为![]() ;
;
②∵直线AB向上平移t个单位得到A′B′,
∴B′(4,t),
易得直线AB′的解析式为y=![]() tx+
tx+![]() t,
t,
解方程组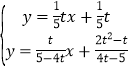 得
得 ,则G(
,则G(![]() ),
),
∴点G的横坐标为定值,点G在直线x=![]() 上,
上,
而0≤t≤2,
∴点G经过的路径的长为1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=![]() ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共享单车被誉为“新四大发明”之一,如图1所示是某公司2017年向信阳市场提供的一种共享自行车的实物图,车架档AC与CD的长分别为45 cm,60 cm,AC⊥CD,座杆CE的长为20 cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离.(结果精确到1 cm,参考数据:sin75°≈0.965 9,cos75°≈0.258 8,tan75°≈3.732 1)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=8,BE=2.则AB2﹣AC2的值为( )

A. 4 B. 6 C. 10 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两块完全一样的含30°角的直角三角板,将它们重叠在一起并绕其较长直角边的中点M转动,使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C.已知AC=4,则这两块直角三角板顶点A、A′之间的距离等于___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,新能源汽车以其舒适环保、节能经济的优势受到热捧,随之而来的就是新能汽车销量的急速增加,当前市场上新能漂汽车从动力上分纯电动和混合动力两种,从用途上又分为乘用式和商用式两种,据中国汽车工业协会提供的信息,2017年全年新能源乘用车的累计销量为57.9万辆,其中,纯电动乘用车销量为46.8万辆,混合动力乘用车销量为11.1万辆; 2017年全年新能源商用车的累计销量为19.8万辆,其中,纯电动商用车销量为18.4万辆,混合动力商用车销量为1.4万辆,请根据以上材料解答下列问题:
(1)请用统计表表示我国2017年新能源汽车各类车型销量情况;
(2)小颖根据上述信息,计算出2017年我国新能源各类车型总销量为77.7万辆,并绘制了“2017年我国新能源汽车四类车型销量比例”的扇形统计图,如图1,请你将该图补充完整(其中的百分数精确到0.1%);

(3)2017年我国新能源乘用车销量最高的十个城市排名情况如图2,请根据图2中信息写出这些城市新能源乘用车销售情况的特点(写出一条即可);
(4)数据显示,2018年1~3月的新能源乘用车总销量排行榜上位居前四的厂家是比亚迪、北汽、上汽、江准,参加社会实践的大学生小王想对其中两个厂家进行深入调研,他将四个完全相同的乒乓球进行编号(用“1,2,3,4”依次对应上述四个厂家),并将乒乓球放入不透明的袋子中搅匀,从中一次拿出两个乒乓球,根据乒乓球上的编号决定要调研的厂家.求小王恰好调研“比亚迪”和“江淮”这两个厂家的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
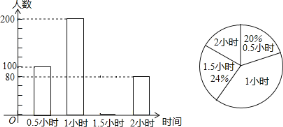
(1)被抽样调查的学生有______人,并补全条形统计图;
(2)每天户外活动时间的中位数是______(小时);
(3)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
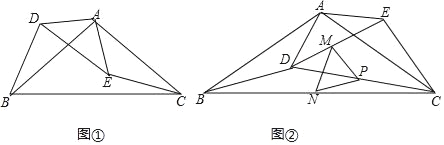
【题目】如图①,在等腰△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE=120°.
(1)求证:△ABD≌△ACE;
(2)把△ADE绕点A逆时针方向旋转到图②的位置,连接CD,点M、P、N分别为DE、DC、BC的中点,连接MN、PN、PM,判断△PMN的形状,并说明理由;
(3)在(2)中,把△ADE绕点A在平面内自由旋转,若AD=4,AB=6,请分别求出△PMN周长的最小值与最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O为△ABC的外接圆,BC为⊙O的直径,AE为⊙O的切线,过点B作BD⊥AE于D.
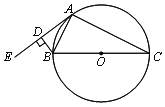
(1)求证:∠DBA=∠ABC;
(2)如果BD=1,tan∠BAD=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com