
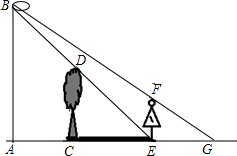
 如图,小彬和小颖放学回家时发现路边一棵小树在路灯下的影子很清晰,他们想利用所学知识,测量一下小树的高度,于是通过步测,测得小树CD底部离路灯杆AB底部8米,树影CE长8米,小颖身高1.6米,她走到树影顶端E处,让小彬测得她在同一路灯下的影子EG长为4米.
如图,小彬和小颖放学回家时发现路边一棵小树在路灯下的影子很清晰,他们想利用所学知识,测量一下小树的高度,于是通过步测,测得小树CD底部离路灯杆AB底部8米,树影CE长8米,小颖身高1.6米,她走到树影顶端E处,让小彬测得她在同一路灯下的影子EG长为4米.分析 (1)根据题意得出△EFG∽△ABG,进而利用相似三角形的性质得出AB的长;
(2)根据题意得出△ABE∽△DCE,进而利用相似三角形的性质得出DC的长.
解答 解:(1)由题意可得:
△EFG∽△ABG,
则$\frac{AB}{EF}=\frac{AG}{EG}$,
∵AG=8+8+4=20,EF=1.6,EG=4,
∴$\frac{AB}{1.6}$=$\frac{20}{4}$,
解得:AB=8.
答:路灯AB高为8米;
(2)由题意可得:
△ABE∽△DCE,
则$\frac{DC}{AB}=\frac{CE}{AE}$,
∵AB=8,CE=8,AE=8+8=16,
∴$\frac{DC}{8}$=$\frac{8}{16}$,
解得:DC=4.
答:小树DC高为4米.
点评 此题主要考查了相似三角形的应用,正确掌握相似三角形的判定方法是解题关键.


科目:初中数学 来源: 题型:解答题
 小亮和爸爸上山游玩,小亮乘坐缆车,爸爸步行,两人相约在山顶的缆车终点会合.已知爸爸行走到缆车终点的路程是缆车到山顶的线路长的2倍,小亮在爸爸出发后50分钟才乘上缆车,缆车的平均速度为180米/分钟.设爸爸出发x 分钟后行走的路程为y米.图中的折线表示爸爸在整个行走过程中y随x的变化关系.
小亮和爸爸上山游玩,小亮乘坐缆车,爸爸步行,两人相约在山顶的缆车终点会合.已知爸爸行走到缆车终点的路程是缆车到山顶的线路长的2倍,小亮在爸爸出发后50分钟才乘上缆车,缆车的平均速度为180米/分钟.设爸爸出发x 分钟后行走的路程为y米.图中的折线表示爸爸在整个行走过程中y随x的变化关系.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
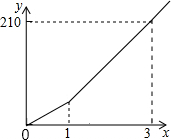 一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )
一辆汽车在行驶过程中,路程y(千米)与时间x(小时)之间的函数关系如图4所示,已知开始1小时的行驶速度是60千米/时,那么1小时以后的速度是( )| A. | 70千米/时 | B. | 75千米/时 | C. | 105千米/时 | D. | 210千米/时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
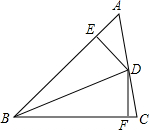 如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.
如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com