
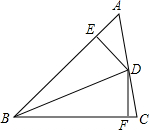
 如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.
如图,BD是△ABC的角平分线,DE⊥AB,DF⊥BC垂足分别为E、F.分析 (1)由角平分线的对称性直接证明△DBE≌△DBF即可;
(2)先算出三角形ABD的面积,再得出三角形BCD的面积,高DF=DE=5,从而直接算出BC.
解答 (1)证明:∵DE⊥AB,DF⊥BC,
∴∠BED=∠BFD=90°,
∵BD是△ABC的角平分线,
∴∠EBD=∠FBD,
又∵BD=BD,
∴△DBE≌△DBF,
∴BE=BF;
(2)解:∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,
∴DF=DE=5,
∴${S}_{△ABD}=\frac{1}{2}AB•DE=40$,
∴${S}_{△BCD}=\frac{1}{2}BC•DF$=70-40=30,
∴BC=12.
故答案为12.
点评 本题主要考查了角平分线的性质、全等三角形的判定与性质、面积法求线段长度,难度中等.熟练掌握角平分线的性质是解答本题的关键.


科目:初中数学 来源: 题型:解答题
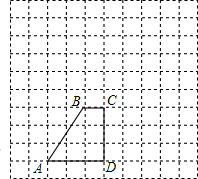 (1)如图在10×10的方格纸中,梯形ABCD是直角梯形,请在图中以CD为对称轴画一个关于直线CD对称的直角梯形EFCD,使它与梯形ABCD构成一个等腰梯形AEFB.(不要求写作法)
(1)如图在10×10的方格纸中,梯形ABCD是直角梯形,请在图中以CD为对称轴画一个关于直线CD对称的直角梯形EFCD,使它与梯形ABCD构成一个等腰梯形AEFB.(不要求写作法)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
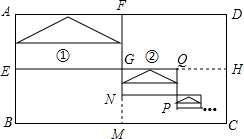 如图,在矩形ABCD中,AD=4,AB=2,连接其对边中点,得到四个矩形,顺次连接AF、FG、AE三边的中点,得到三角形①;连接矩形GMCH对边的中点,又得到四个矩形,顺次连接GQ、QP、GN三边的中点,得到三角形②;…;如此操作下去,得到三角形
如图,在矩形ABCD中,AD=4,AB=2,连接其对边中点,得到四个矩形,顺次连接AF、FG、AE三边的中点,得到三角形①;连接矩形GMCH对边的中点,又得到四个矩形,顺次连接GQ、QP、GN三边的中点,得到三角形②;…;如此操作下去,得到三角形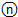 ,则三角形
,则三角形 的面积为$\frac{1}{{2}^{2n-1}}$.
的面积为$\frac{1}{{2}^{2n-1}}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
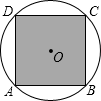 如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )
如图,正方形ABCD内接于⊙O,⊙O的直径为$\sqrt{2}$分米,若在这个圆面上随意抛一粒豆子,则豆子落在正方形ABCD内的概率是( )| A. | $\frac{2}{π}$ | B. | $\frac{π}{2}$ | C. | $\frac{1}{2π}$ | D. | $\sqrt{2}π$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
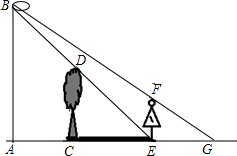 如图,小彬和小颖放学回家时发现路边一棵小树在路灯下的影子很清晰,他们想利用所学知识,测量一下小树的高度,于是通过步测,测得小树CD底部离路灯杆AB底部8米,树影CE长8米,小颖身高1.6米,她走到树影顶端E处,让小彬测得她在同一路灯下的影子EG长为4米.
如图,小彬和小颖放学回家时发现路边一棵小树在路灯下的影子很清晰,他们想利用所学知识,测量一下小树的高度,于是通过步测,测得小树CD底部离路灯杆AB底部8米,树影CE长8米,小颖身高1.6米,她走到树影顶端E处,让小彬测得她在同一路灯下的影子EG长为4米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
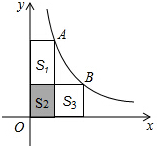 如图,A、B两点在反比例函数y=$\frac{4}{x}$的图象上,分别过A、B两点向坐标轴作垂线段,已知S2的面积为1,则S1+S3的面积为( )
如图,A、B两点在反比例函数y=$\frac{4}{x}$的图象上,分别过A、B两点向坐标轴作垂线段,已知S2的面积为1,则S1+S3的面积为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-3) | B. | (2,-3) | C. | (2,3) | D. | (-1,-6) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\sqrt{(-13)^{2}}$=13 | B. | $\sqrt{(-6)^{2}}$=-6 | C. | -$\sqrt{25}$=-5 | D. | $\sqrt{9}$=±3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com