
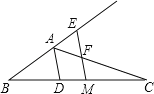
【题目】如图,已知△ABC,AD平分∠BAC交BC于点D,BC的中点为M,ME∥AD,交BA的延长线于点E,交AC于点F.
(1)求证:AE=AF;
(2)求证:BE=![]() (AB+AC).
(AB+AC).
【答案】(1)详见解析;(2)详见解析.
【解析】
试题分析:(1)根据角平分线的性质及平行线的性质易∠AEF=∠AFE,即可得AE=AF;(2)作CG∥EM,交BA的延长线于G,已知AC=AG,根据三角形中位线定理的推论证明BE=EG,再利用三角形的中位线定理即可证得结论.
试题解析:
(1)∵DA平分∠BAC,
∴∠BAD=∠CAD,
∵AD∥EM,
∴∠BAD=∠AEF,∠CAD=∠AFE,
∴∠AEF=∠AFE,
∴AE=AF.
(2)作CG∥EM,交BA的延长线于G.
∵EF∥CG,
∴∠G=∠AEF,∠ACG=∠AFE,
∵∠AEF=∠AFE,
∴∠G=∠ACG,
∴AG=AC,
∵BM=CM.EM∥CG,
∴BE=EG,
∴BE=![]() BG=
BG=![]() (BA+AG)=
(BA+AG)=![]() (AB+AC).
(AB+AC).



科目:初中数学 来源: 题型:
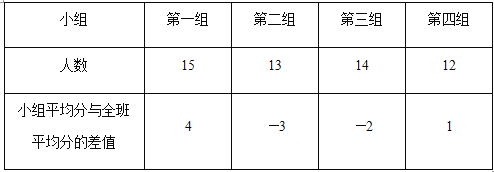
【题目】某班举办数学知识比赛,共分五个小组,其中四个小组的成绩如表所示,请问
(1)这四个小组的总平均分比全班的平均分高还是低?为什么?
(2)据(1)你能否判断第五组的成绩比全班平均分高,还是低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】亮亮做抛硬币的实验,共抛了10次,3次正面朝上,7次反面朝上,准确的说法是( )
A. 正面朝上的频数是3 B. 正面朝上的频率是3
C. 反面朝上的频率是7 D. 正面朝上的频数是0.3
查看答案和解析>>
科目:初中数学 来源: 题型:
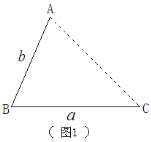
【题目】(1)发现
如图1,点A为线段BC外一动点,且BC=![]() ,AB=
,AB=![]() .
.
填空:当点A位于__________________时,线段AC的长取得最大值,且最大值为_____________.
(用含![]() ,
,![]() 的式子表示)
的式子表示)
(2)应用
点A为线段BC外一动点,且BC=3,AB=1.如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.

(3)拓展
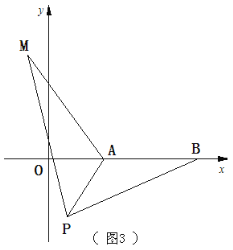
如图3,在平面直角坐标系中,点A的坐标为(2 , 0),点B的坐标为(5 , 0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°.请直接写出线段AM长的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2+4x+3化成顶点式,变形正确的是( )
A. y=(x﹣2)2﹣1 B. y=(x+1)(x+3)
C. y=(x﹣2)2+1 D. y=(x+2)2﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于角的说法正确的是( )
A. 两条射线组成的图形叫做角 B. 角的大小与这个角的两边的长短无关
C. 延长一个角的两边 D. 角的两边是射线,所以角不可度量
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com