Question

13．2015年11月11日，一年一度“双十一”购物狂欢日盛大启幕，“剁手党”们纷纷清空自己的购物车，其中不乏冲动消费者，某校初三1班的数学兴趣小组以“理性购物，拒绝冲动消费”为主题对消费行为进行调查．按购物数量x（件）分为以下4类：A（x≤3），B（x=4），C（x=5），D（x≥6），根据调查结果制作了如下两图统计图（不完整），已知购买4件商品的消费者中，理性购物人数所占比例为80%，根据图中信息回答下列问题：

（1）本次调查的总人数为60人，理性购物者购物件数的中位数为4件；
（2）补全条形统计图；
（3）小张在“双十一”共购进7件商品，其中4件服装购自“天猫商城”，3件电子产品购自“京东商城”，由于购买时存在冲动消费，小张决定从服装和电子产品中各随机选择1件进行退货，已知“天猫商城”购买的4件服装中仅1件支持退货，“京东商城”购买的电子产品中仅2件支持退货．请用列表或树状图的方法，求小张选出的2件商品均能退货的概率．

Answer 1

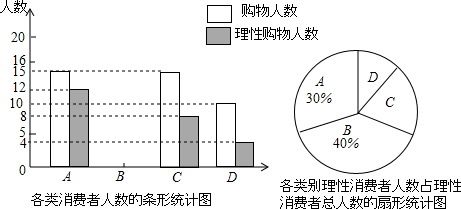
分析 （1）利用条形统计图和扇形图，利用A类的理性购物人数除以它所占的百分比得到理性购物人数的总人数为40人，再利用B类理性购物人数所占的百分比可计算出B类理性购物人数为16人，接着利用购买4件商品的消费者中，理性购物人数所占比例为80%可计算出B类购物人数，然后把四类购物人数相加即可得到本次调查的总人数，再利用中位数定义得到理性购物者购物件数的中位数；
（2）补全条形统计图；
（3）用1、2、3、4表示购自“天猫商城的4件服装，且4为支持退货的服装；3件电子产品用5、6、7表示，且6、7为支持退货的电子产品，画树状图展示所有12种等可能的结果数，再找出2件商品均能退货的结果数，然后根据概率公式求解．

解答 解：（1）理性购物的总人数为12÷30%=40（人），则B类理性购物人数为40×40%=16，
所以B类购物人数为16÷80%=20（人），
本次调查的总人数为15+20+15+10=60（人），
理性购物者购物件数的中位数为 4件；
（2）全条形统计图为：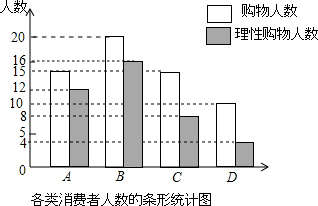

（3）用1、2、3、4表示购自“天猫商城的4件服装，且4为支持退货的服装；3件电子产品用5、6、7表示，且6、7为支持退货的电子产品，
画树状图为：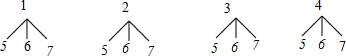

共有12种等可能的结果数，其中2件商品均能退货的结果数2，
所以2件商品均能退货的概率=$\frac{2}{12}$=$\frac{1}{6}$．

点评 本题考查了列表法与树状图法：利用列表法和树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，求出概率．也考查了统计图．