
 ��ͼ��һ�κ���y=-x+4��ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B������A��x��Ĵ���l����PΪֱ��l�ϵĶ��㣬��QΪֱ��AB���OAP���Բ�Ľ��㣬��P��Q���A�����غϣ�
��ͼ��һ�κ���y=-x+4��ͼ����x�ᡢy��ֱ��ཻ�ڵ�A��B������A��x��Ĵ���l����PΪֱ��l�ϵĶ��㣬��QΪֱ��AB���OAP���Բ�Ľ��㣬��P��Q���A�����غϣ����� ��1����y=0����y=-x+4�����x��ֵ���Ӷ��õ���A�����ꣻ
��2�����ȸ������⻭��ͼ�Σ�Ȼ����Rt��BOA�У��ɹ��ɶ����ã�AB�ij��ȣ�Ȼ����ȫ�������ε��������QA�ij��ȣ��Ӷ��õ�BQ�ij���Ȼ�����PA=BQ���PA�ij��ȣ��Ӷ�����õ�P�����ꣻ
��3�����ȸ������⻭��ͼ�Σ���AP=m���ɡ�OAM�ס�PAO�������AM�ij��ȣ�Ȼ����ݹ��ɶ����������Բ��ֱ�����ú�m��ʽ�ӱ�ʾ����Ȼ������Բ�������ʽ�����Բ��������������������ʽ��⼴�ɣ�
��� �⣨1����y=0���ã�-x+4=0�����x=4��
����A��������4��0����
��2�����ڣ�
���ɣ���һ�����������ͼһ��ʾ��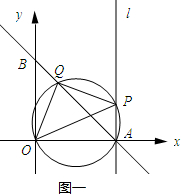
�ߡ�OBA=��BAP���������Ƕ�Ӧ�ǣ�
��BQ=PA��
��x=0����y=-x+4�ã�y=4��
��OB=4��
�ɣ�1����֪OA=4��
��Rt��BOA�У��ɹ��ɶ����ã�AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=4$\sqrt{2}$��
�ߡ�BOQ�ա�AQP��
��QA=OB=4��BQ=PA��
��BQ=AB-AQ=4$\sqrt{2}$-4��
��PA=4$\sqrt{2}$-4��
���P��������4��4$\sqrt{2}$-4����
�ڶ������������ͼ����ʾ��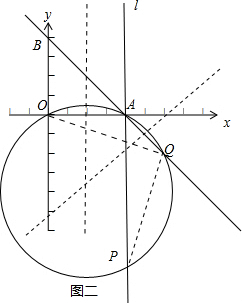
�ߡ�OQB�ա�APQ��
��AQ=BO=4��AB=$\sqrt{{4}^{2}+{4}^{2}}=4\sqrt{2}$��BQ=AP��
��BQ=AB+AQ=$4\sqrt{2}+4$��
��AP=4$\sqrt{2}+4$��
���P����������4��-4$\sqrt{2}-4$����
���Ͽɵã���P������Ϊ����4��$4\sqrt{2}-4$����4��$-4\sqrt{2}-4$����
��3����ͼ��ʾ��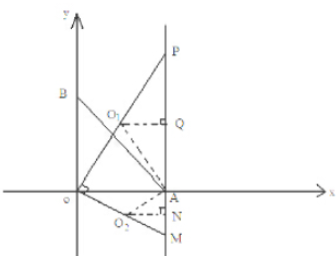
��PA=a��MA=b����OAP���Բ��Բ��ΪO1����OAM�����Բ��Բ��ΪO2��
��OP2=OA2+PA2=42+a2=16+a2��OM2=OA2+MA2=42+b2=16+b2��
��Rt��POM��PM2=OP2+OM2=a2+16+b2+16��
�֡�PM2=��PA+AM��2=��a+b��2=a2+2ab+b2��
��ab=16��
��O1A2=O1Q2+QA2=��$\frac{OA}{2}$��2+��$\frac{PA}{2}$��2=$\frac{1}{4}$a2+4��O2A2=O2N2+NA2=��$\frac{OA}{2}$��2+��$\frac{MA}{2}$��2=$\frac{1}{4}$b2+4��
��S1=��O1A2=��$\frac{1}{4}$a2+4����S2=��O2A2=��$\frac{1}{4}$b2+4����
��$\frac{1}{{S}_{1}}+\frac{1}{{S}_{2}}$=$\frac{{S}_{1}+{S}_{2}}{{S}_{1}{S}_{2}}$=$\frac{����\frac{1}{4}{a}^{2}+4��+����\frac{1}{4}{b}^{2}+4��}{����\frac{1}{4}{a}^{2}+4��������\frac{1}{4}{b}^{2}+4��}$=$\frac{4}{��}$��$\frac{{a}^{2}+{16+b}^{2}+16}{16{a}^{2}+16{b}^{2}+1{6}^{2}+1{6}^{2}}$=$\frac{1}{4��}$��
���� ������Ҫ�������ȫ�������ε����ʣ����������ε����ʺ��ж��Լ����ɶ�����һ�κ������ۺ�Ӧ�ã��������⻭��ͼ�Σ�����ȫ�������κ����������ε����ʺ��ж����AM��PA�ij����ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
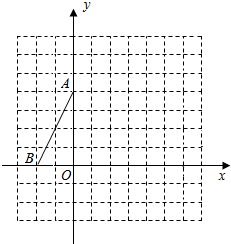 ��ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬��A��B������ֱ�ΪA��0��4����B��-2��0��������AB��
��ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬��A��B������ֱ�ΪA��0��4����B��-2��0��������AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com