
分析 (1)(2)小题是加减混合运算,先统一成加法,再用加法法则进行运算;
(3)(4)(5)小题是运用法则;先算乘方,再算乘除,最后再算加减.
解答 解:(1)-7+13-6+20
=-13+13+20
=20;
(2)(-49)-(+91)-(-5)+(-9)
=-91-9-49+5
=-149+5
=-144;
(3)(-18)×(-$\frac{1}{9}$+$\frac{2}{3}$-$\frac{1}{6}$)
=-18×(-$\frac{1}{9}$)-18×$\frac{2}{3}$-18×$(-\frac{1}{6})$
=2-12+3
=-7;
(4)-24-$\frac{1}{2}$×[5-(-3)2]
=-16-$\frac{1}{2}×(5-9)$
=-16+2
=-14;
(5)(-12$\frac{2}{3}$)÷1.4-(-8$\frac{1}{3}$)÷(-1.4)+9$\frac{1}{3}$÷1.4
=$(-12\frac{2}{3}+8\frac{1}{3}+9\frac{1}{3})×\frac{5}{7}$
=$\frac{25}{7}$.
点评 此题考查有理数的混合计算,解此题的关键是正确运用有理数的混合运算法则:有乘方先算乘方,再算乘除,最后算加减.以及利用绝对值的法则.特别应注意结果的符号.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=-x+4的图象与x轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB与△OAP外接圆的交点,点P、Q与点A都不重合.
如图,一次函数y=-x+4的图象与x轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB与△OAP外接圆的交点,点P、Q与点A都不重合.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
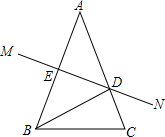 已知:如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
已知:如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6,8,12 | B. | 1,4,$\sqrt{3}$ | C. | 3,4,5 | D. | 2,2,$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°
如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com