
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,一次函数y=-x+4的图象与x轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB与△OAP外接圆的交点,点P、Q与点A都不重合.
如图,一次函数y=-x+4的图象与x轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB与△OAP外接圆的交点,点P、Q与点A都不重合.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6,8,12 | B. | 1,4,$\sqrt{3}$ | C. | 3,4,5 | D. | 2,2,$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°
如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°查看答案和解析>>
科目:初中数学 来源: 题型:选择题
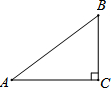 已知,如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinB的值是( )
已知,如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,则sinB的值是( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 2015年10月18日起1008次列车时刻表 | |||
| 始发点 | 发车时间 | 终点站 | 到站时间 |
| A站 | 上午8:20 | B站 | 次日12:20 |
| 2014年1008次列车时刻表 | |||
| 始发点 | 发车时间 | 终点站 | 到站时间 |
| A站 | 下午14:30 | B站 | 第三日8:30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
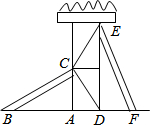 某游乐场有两个长度相同的滑梯,要想使左边滑梯BC的高度AC与右边滑梯EF的水平方向的长度DF相等,则两个滑梯的倾斜角∠ABC与∠DFE的大小必须满足什么关系?说明理由.
某游乐场有两个长度相同的滑梯,要想使左边滑梯BC的高度AC与右边滑梯EF的水平方向的长度DF相等,则两个滑梯的倾斜角∠ABC与∠DFE的大小必须满足什么关系?说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com