
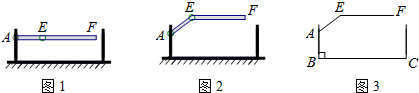
分析 过点A作BC的平行线AG,过点E作EH⊥AG于H,则∠BAG=90°,∠EHA=90°.先求出∠AEH=53°,则∠EAH=37°,然后在△EAH中,利用正弦函数的定义得出EH=AE•sin∠EAH,则栏杆EF段距离地面的高度为:AB+EH,代入数值计算即可.
解答 解:如图,过点A作BC的平行线AG,过点E作EH⊥AG于H,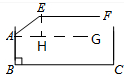
则∠EHG=∠HEF=90°,
∵∠AEF=143°,
∴∠AEH=∠AEF-∠HEF=53°,
∠EAH=37°,
在△EAH中,∠EHA=90°,∠EAH=37°,AE=1.3米,
∴EH=AE•sin∠EAH≈1.3×0.60=0.78(米),
∵AB=1.3米,
∴AB+EH≈1.3+0.78=2.08≈2.1(米);
答:适合该地下车库的车辆限高标志牌约为2.1米.
点评 本题考查了解直角三角形在实际中的应用,难度适中.关键是通过作辅助线,构造直角三角形,把实际问题转化为数学问题加以计算.


科目:初中数学 来源: 题型:解答题
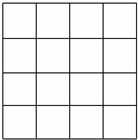 如图,正方形网格中的每个小正方形边长都是1,请在图中画出△ABC使得A、B、C三点都在小正方形的顶点且AB=AC=$\sqrt{5}$,BC=$\sqrt{2}$,并求出所画三角形的面积.
如图,正方形网格中的每个小正方形边长都是1,请在图中画出△ABC使得A、B、C三点都在小正方形的顶点且AB=AC=$\sqrt{5}$,BC=$\sqrt{2}$,并求出所画三角形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
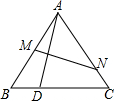 如图,点M、N分别是等边三角形ABC中AB,AC边上的点,点A关于MN的对称点落在BC边上的点D处.若$\frac{BD}{DC}$=$\frac{2}{3}$,则$\frac{AM}{AN}$的值$\frac{7}{8}$.
如图,点M、N分别是等边三角形ABC中AB,AC边上的点,点A关于MN的对称点落在BC边上的点D处.若$\frac{BD}{DC}$=$\frac{2}{3}$,则$\frac{AM}{AN}$的值$\frac{7}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=-x+4的图象与x轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB与△OAP外接圆的交点,点P、Q与点A都不重合.
如图,一次函数y=-x+4的图象与x轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB与△OAP外接圆的交点,点P、Q与点A都不重合.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°
如图,已知:在四边形ABCD中,过C作CE⊥AB于E,并且CD=CB,∠ABC+∠ADC=180°查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com