
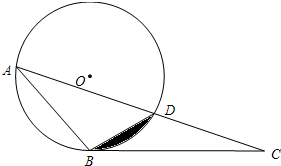
 如图,△ABC中,⊙O经过A、B两点,且交AC于点D,∠DBC=∠BAC.
如图,△ABC中,⊙O经过A、B两点,且交AC于点D,∠DBC=∠BAC. 解:(1)BC是⊙O的切线.理由如下:
解:(1)BC是⊙O的切线.理由如下:
| ||
| 4 |
| 3 |
| 60π×42 |
| 360 |
| 8 |
| 3 |
| 8 |
| 3 |
| 3 |


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
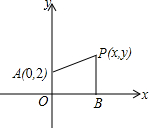 如图,点P(x,y)为平面直角坐标系内一点,PB⊥x轴,垂足为B,点A的坐标为(0,2),若PA=PB,则以下结论正确的是( )
如图,点P(x,y)为平面直角坐标系内一点,PB⊥x轴,垂足为B,点A的坐标为(0,2),若PA=PB,则以下结论正确的是( )A、点P在直线y=
| ||
B、点P在抛物线y=
| ||
C、点P在抛物线y=
| ||
D、点P在抛物线y=
|
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,某居民楼A与公路MN相距60m(AB=60m),在公路MN上行驶的汽车在距居民楼A100m的点P处就可使其受到噪音的影响,求在公路上以10m/s的速度行驶的汽车给居民楼A的居民带来多长时间的噪音影响.
如图,某居民楼A与公路MN相距60m(AB=60m),在公路MN上行驶的汽车在距居民楼A100m的点P处就可使其受到噪音的影响,求在公路上以10m/s的速度行驶的汽车给居民楼A的居民带来多长时间的噪音影响.查看答案和解析>>
科目:初中数学 来源: 题型:
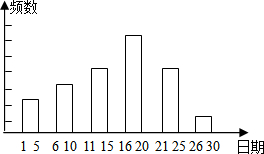 某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的频数是12.请你回答:
某校九年级一班的暑假活动安排中,有一项是小制作评比.作品上交时限为8月1日至30日,班委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的频数是12.请你回答:查看答案和解析>>
科目:初中数学 来源: 题型:
| n+7 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com