
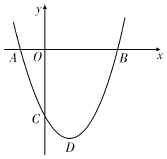
【题目】如图,已知拋物线![]() 经过A(-1,0),B(3,0)两点,与y轴相交于点C,该拋物线的顶点为点D.
经过A(-1,0),B(3,0)两点,与y轴相交于点C,该拋物线的顶点为点D.
(1)求该拋物线的解析式及点D的坐标;
(2)连接AC,CD,DB,BC,设△AOC,△BOC,△BCD的面积分别为 S1,S2,S3,求证:![]() .
.
(3)点M是线段AB上一动点(不包括点A和点B),过点M作MN//BC交AC于点N,连接MC,是否存在点M使∠AMN=∠ACM?若存在,求出点M的坐标和此时直线MN的解析式;若不存在,请说明理由.
【答案】(1)点D的坐标为(1,-4);(2)见解析(3)直线MN的解析式为![]() .
.
【解析】
试题
(1)由抛物线![]() 过点A(-1,0),B(3,0)可得其解析式为:
过点A(-1,0),B(3,0)可得其解析式为:![]() ,化简、再配方为顶点式,可得顶点D的坐标;
,化简、再配方为顶点式,可得顶点D的坐标;
(2)连接AC,CD,DB,BC,由(1)中所求解析式可得点C的坐标,这样就可由A、B、C、D、O五点的坐标分别求出三个三角形△AOC,△BOC,△BCD的面积,从而可证得:![]() .
.
(3)由题意可设点M的坐标为(m,0),其中-1<m<3,则AM=m+1;由已知和(2)可求得:AC=![]() ,AB=4;由MN∥BC可得:AM:AB=AN:AC,从而可得解得:AN=
,AB=4;由MN∥BC可得:AM:AB=AN:AC,从而可得解得:AN=![]() ;由∠AMN=∠ACM,∠MAN=∠CAM,可得△AMN∽△ACM,因此:AM:AC=AN:AM,由此可列出关于m的方程,解方程求得m的值即可得到点M的坐标,然后利用已知可求得直线BC的解析式,再由MN∥BC,即可求得直线MN的解析式.
;由∠AMN=∠ACM,∠MAN=∠CAM,可得△AMN∽△ACM,因此:AM:AC=AN:AM,由此可列出关于m的方程,解方程求得m的值即可得到点M的坐标,然后利用已知可求得直线BC的解析式,再由MN∥BC,即可求得直线MN的解析式.
试题解析:
(1)∵抛物线![]() 过点A(-1,0),B(3,0)
过点A(-1,0),B(3,0)
∴抛物线的解析式为y=(x+1)(x-3),即y=x2-2x-3.
∵y=x2-2x-3=(x-1)2-4,
∴点D的坐标为(1,-4)
(2)如下图,
∵当x=0时,y=x2-2x-3=-3,
∴C(0,-3),
又∵A(-1,0),B(3,0),
∴![]() ,
,
![]() ,
,
![]() .
.
∴![]() .
.
∴△BCD为直角三角形,![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
(3)存在点M使∠AMN=∠ACM.
设点M的坐标为(m,0)(-1<m<3),则MA=m+1,
![]() ,AB=1+3=4,
,AB=1+3=4,
∵MN//BC,
∴AM:AB=AN:AC,即(m+1):AN=4:![]() .
.
解得AN=![]() .
.
∵∠AMN=∠ACM,∠MAN=∠CAM,
∴△AMN∽△ACM.
∴AM:AC=AN:AM.即(m+1)2=![]() .
.
解得m1=-1(不合题意,舍去),![]() .
.
∴点M的坐标为![]() .
.
设直线BC的解析式为y=kx+b.
把B(3,0),C(0,-3)代入,得![]() 解得
解得![]()
∴直线BC的解析式为y=x-3.
又∵MN//BC,
∴设直线MN的解析式为y=x+n.
把点M的坐标![]() 代入,得
代入,得![]() .
.
∴直线MN的解析式为![]() .
.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:
【题目】儿童节期间,某公园游戏场举行一场活动.有一种游戏的规则是:在一个装有8个红球和若干白球(每个球除颜色外,其他都相同)的袋中,随机摸一个球,摸到一个红球就得到一个海宝玩具.已知参加这种游戏的儿童有40 000人,公园游戏场发放海宝玩具8 000个.
(1)求参加此次活动得到海宝玩具的频率?
(2)请你估计袋中白球的数量接近多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有形状、大小和质地都相同的四张卡片,正面分别写有A,B,C,D和一个等式,将这四张卡片背面向上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张.
![]()
(1)用画树状图或列表的方法表示抽取两张卡片可能出现的所有情况(结果用A,B,C,D表示).
(2)小明和小强按下面规则做游戏:抽取的两张卡片上若等式都不成立,则小明胜;若至少有一个等式成立,则小强胜.你认为这个游戏公平吗?若公平,请说明理由;若不公平,则这个规则对谁有利?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=![]() ,将△ABC绕点P旋转180°,得到△MCB.
,将△ABC绕点P旋转180°,得到△MCB.

(1)求B、C两点的坐标;
(2)请在图中画出线段MB、MC,并判断四边形ACMB的形状(不必证明),求出点M的坐标;
(3)动直线l从与BM重合的位置开始绕点B顺时针旋转,到与BC重合时停止,设直线l与CM交点为E,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.请问在旋转过程中∠MQG的大小是否变化?若不变,求出∠MQG的度数;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+(2﹣a)x﹣2(a>0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.给出下列结论:
①在a>0的条件下,无论a取何值,点A是一个定点;
②在a>0的条件下,无论a取何值,抛物线的对称轴一定位于y轴的左侧;
③y的最小值不大于﹣2;
④若AB=AC,则a=![]() .
.
其中正确的结论有( )个.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
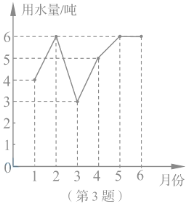
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线上,抛物线m经过点B、C(p+4,q),且它的顶点N在直线l上.
(1)若B(-2,1),
①请在平面直角坐标系中画出直线l与抛物线m的示意图;
②设抛物线m上的点Q的模坐标为e(-2≤e≤0)过点Q作x轴的垂线,与直线l交于点H.若QH=d,当d随e的增大面增大时,求e的取值范围;
(2)抛物线m与y轴交于点F,当抛物线m与x轴有唯一交点时,判断△NOF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC与△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,AC=BC=4,AD=DE,点F是BE的中点,连接DF,CF.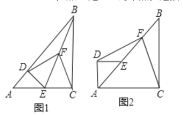
(1)如图1,当点D在AB上,且点E是AC的中点时,求CF的长.
(2)如图1,若点D落在AB上,点E落在AC上,证明:DF⊥CF.
(3)如图2,当AD⊥AC,且E点落在AC上时,判断DF与CF之间的关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com