Question

11．已知△ABC，D、E是射线BC上的两点，且BD=AB，CE=AC．
（1）若AB=AC，且∠BAC=90°（如图），求证：AE²=BE•DE；
（2）若△ABC是直角三角形，且AE²=BE•DE，求∠ABC的度数．（如果需要，自己画出符合条件的大致图形）

Answer 1

分析 （1）如图1，根据等边对等角依次求出∠B、∠E、∠DAC、∠CAE、∠DAE的度数，证明∠EAD=∠B，根据两角对应相等证明△EAD∽△EBA，得比例式可得结论；
（2）分三种情况讨论：
①当∠BAC=90°时，如图1，证明△ADE∽△BAE，得∠DAE=∠B，设∠E=x°，根据等量关系：∠ADB=∠DAE+∠E，列方程为45+x=90-2x+x，求出x的值，从而计算出∠ABC的度数；
②当∠ABC=90°时，如图2，因为∠EAD≠∠B，所以此种情况不成立；
③当∠ACB=90°时，如图3，同①，根据∠BAD=∠ADB得：90-x+45-x=90-$\frac{1}{2}$x，得出结论．

解答 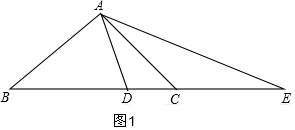证明：（1）如图1，∵AB=AC，∠BAC=90°，
∴∠B=∠BCA=45°，
∠BAD=∠BDA=$\frac{180°-45°}{2}$=67.5°，
∴∠DAC=90°-67.5°=22.5°，
∵AC=CE，
∴∠E=∠CAE=22.5°，
∴∠EAD=45°，
∴∠EAD=∠B，
∵∠E=∠E，
∴△EAD∽△EBA，
∴$\frac{AE}{EB}=\frac{ED}{AE}$，
∴AE²=BE•DE；
（2）若△ABC是直角三角形，分三种情况讨论：
①当∠BAC=90°时，如图1，
∵AE²=BE•DE，
∴$\frac{AE}{BE}=\frac{DE}{AE}$，
∵∠E=∠E，
∴△ADE∽△BAE，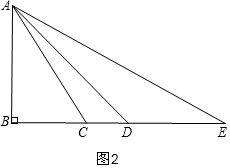
∴∠DAE=∠B，
设∠E=x°，
∵AC=CE，
∴∠CAE=∠E=x°，
∴∠ACB=2x°，
∵∠BAC=90°，
∴∠B=90°-2x°，
∵AB=AD，
∴∠BDA=∠BAD=$\frac{180-（90-2x）}{2}$=45+x，
在△ADE中，∠DAE=∠B=90-2x，
∠ADB=∠DAE+∠E，
45+x=90-2x+x，
x=22.5°，
∴∠ABC=90-2x=45°；
②当∠ABC=90°时，如图2，
∵AE²=BE•DE，∠E=∠E，
∴△ADE∽△BAE，
但图2中，∠EAD≠∠B，
所以此种情况不成立；
③当∠ACB=90°时，如图3，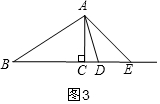
∵AC=CE，
∴∠CAE=∠E=45°，
∵AE²=BE•DE，∠E=∠E，
∴△ADE∽△BAE，
∴∠DAE=∠B，
设∠B=x°，则∠DAE=x°，∠BAC=90°-x°，
∴∠DAC=45°-x°，
∵AB=BD，
∴∠ADB=$\frac{180°-x°}{2}$=90°-$\frac{1}{2}$x°，
由∠BAD=∠ADB得：90-x+45-x=90-$\frac{1}{2}$x，
x=30°，
∴∠ABC=30°，
综上所述：∠ABC=45°或30°．

点评 本题考查了相似三角形、等腰三角形的性质和判定，本题多次运用了等边对等角及三角形的外角定理得出角的大小关系，根据两角对应相等证得三角形相似，从而得出比例式；在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件；对于第二问中的如果△ABC是直角三角形时，要采用分类讨论的思想解决问题，正确画图，设未知数，找到恰当的等量关系列方程求得结论．