Question

13．如图1，在△ACB和△AED中，AC=BC，AE=DE，∠ACB=∠AED=90°，点E在AB上，点D在AC上．
（1）若F是BD的中点，求证：CF=EF；
（2）将图1中的△AED绕点A顺时针旋转，使AE恰好在AC上（如图2）．若F为BD上一点，且CF=EF，求证：BF=DF；
（3）将图1中的△AED绕点A顺时针旋转任意的角度（如图3）．若F是BD的中点．探究CE与EF的数量关系，并证明你的结论．

Answer 1

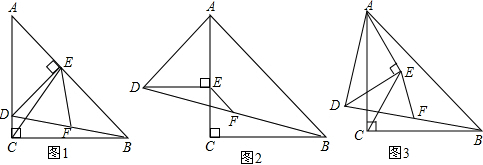
分析 （1）连接CF，直角△DEB中，EF是斜边BD上的中线，因此EF=DF=BF，∠FEB=∠FBE，同理可得出CF=DF=BF，∠FCB=∠FBC，因此CF=EF，
（2）通过证明△EFC是等腰直角三角形来求解．先证△EFC是等腰三角形，证明△DEF和△FGB全等．
（3）通过证明△CFE来得出结论，通过全等三角形来证得CF=FE，证明△MEF和△CFN全等，利用三角形的中位线和直角三角形斜边上的中线，我们不难得出EM=PN$\frac{1}{2}$AD，EC=MF=$\frac{1}{2}$AB，得出四边形AMPN为平行四边形，那么对角就相等，于是90°+∠CNF=90°+∠MEF，因此∠CNF=∠MEF，那么两三角形就全等了．证明∠CFE是直角的过程与（1）完全相同．那么就能得出△CEF是个等腰直角三角形，于是得出的结论与（1）也相同．

解答 （1）证明：如图1，连接CF，

直角△DEB中，EF是斜边BD上的中线，
∴EF=$\frac{1}{2}$BD，
同理可得出CF=$\frac{1}{2}$BD，
∴CF=EF，
（2）（1）中的结论仍然成立．
如图2，连接CF，

延长EF交CB于点G，
∵∠ACB=∠AED=90°，
∴DE∥BC，
∴∠EDF=∠GBF，
又∵∠EFD=∠GFB，DF=BF，
∴△EDF≌△GBF，
∴BF=DF．
（3）（1）中的结论仍然成立．
如图3，

取AD的中点M，连接EM，MF，取AB的中点N，连接FN、CN、CF，
∵DF=BF，
∴FM∥AB，且FM=$\frac{1}{2}$ AB，
∵AE=DE，∠AED=90°，
∴AM=EM，∠AME=90°，
∵CA=CB，∠ACB=90°，
∴CN=AN=$\frac{1}{2}$AB，∠ANC=90°，
∴MF∥AN，FM=AN=CN，
∴四边形MFNA为平行四边形，
∴FN=AM=EM，∠AMF=∠FNA，
∴∠EMF=∠FNC，
∴△EMF≌△FNC，
∴FE=CF，∠EFM=∠FCN，
由MF∥AN，∠ANC=90°，
可得∠CPF=90°，
∴∠FCN+∠PFC=90°，
∴∠EFM+∠PFC=90°，
∴∠EFC=90°，
∴△CEF为等腰直角三角形，
∴∠CEF=45°，
∴CE=$\sqrt{2}$EF．

点评 此题是几何变换综合题，主要考查全等三角形的判定，平行四边形的判定和性质，解本题的关键是通过全等三角形来得出线段的相等，难点是要根据已知条件通过辅助线来构建．