
分析 (1)原式利用单项式乘以多项式法则计算即可得到结果;
(2)原式利用多项式乘以多项式法则计算即可得到结果;
(3)原式利用多项式乘以多项式法则计算即可得到结果;
(4)原式利用多项式乘以多项式法则计算即可得到结果;
(5)原式利用多项式除以单项式法则计算即可得到结果;
(6)原式利用完全平方公式展开即可得到结果.
解答 解:(1)原式=$\frac{\sqrt{6}}{2}$-$\frac{\sqrt{6}}{3}$=$\frac{\sqrt{6}}{6}$;
(2)原式=6+4$\sqrt{6}$-6$\sqrt{6}$-24=-2$\sqrt{6}$-18;
(3)原式=$\frac{5}{2}$-$\frac{5\sqrt{3}}{3}$-3$\sqrt{3}$+6=$\frac{17}{2}$-$\frac{14\sqrt{3}}{3}$;
(4)原式=$\sqrt{6}$-$\frac{3}{4}$+8-$\sqrt{6}$=7$\frac{1}{4}$;
(5)原式=20$\sqrt{2}$-9$\sqrt{2}$+4$\sqrt{2}$=15$\sqrt{2}$;
(6)原式=12+72-24$\sqrt{6}$.
点评 此题考查了二次根式的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
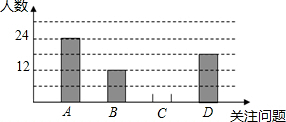 随着人类的进步,人们越来越关注周围环境的变化,社会也积极呼吁大家都为环境尽份力.小明积极学习与宣传,并从四个方面:A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表和统计图:
随着人类的进步,人们越来越关注周围环境的变化,社会也积极呼吁大家都为环境尽份力.小明积极学习与宣传,并从四个方面:A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表和统计图:| 关注问题 | 频数 | 频率 |
| A | 24 | B |
| B | 12 | 0.2 |
| C | N | 0.1 |
| D | 18 | M |
| 合计 | a | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
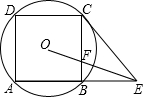 如图,四边形ABCD是⊙O的内接正方形,延长AB至点P,使BP=AB,连接PC.
如图,四边形ABCD是⊙O的内接正方形,延长AB至点P,使BP=AB,连接PC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com