
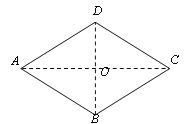
【题目】已知:如图,四边形ABCD是菱形,AB=AD.
求证:(1) AB=BC=CD=DA
(2) AC⊥DB
(3) ∠ADB=∠CDB,∠ABD=∠CBD,∠DAC=∠BAC,∠DCA=∠BCA
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)根据菱形定义:一组邻边相等的平行四边形是菱形即可解答;(2)利用SSS证明△ADO≌△CDO,可得:∠AOD=∠COD,又因为∠AOD+∠COD=180°,所以∠AOD=∠COD=90°即可得出AC⊥DB;(3)由△ADO≌△CDO,再根据全等三角形对应角相等,两直线平行,内错角相等即可解答.
证明:(1)∵四边形ABCD是菱形,∴AB=CD,AD=CB.
又∵AB=AD,∴AB=BC=CD=DA.
(2)在△ADO和△CDO中,
∵DA=DC,DO=DO,AO=CO,∴△ADO≌△CDO. ∴∠AOD=∠COD.
∵∠AOD+∠COD=180°,∴∠AOD=∠COD=90°. ∴AC⊥DB.
(3) ∵△ADO≌△CDO, ∴∠ADB=∠CDB,∠DAC=∠DCA.
∵AB∥CD,AD∥CB,
∴∠ADB=∠CBD,∠CDB=∠ABD,∠DAC=∠BCA,∠DCA=∠BAC.
∴∠ADB=∠CDB,∠ABD=∠CBD,∠DAC=∠BAC,∠DCA=∠BCA.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点E,F在边AB上,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处.

(1)求∠ECF的度数;
(2)若CE=4,B'F=1,求线段BC的长和△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB,以O为圆心,以任意长为半径作弧,分别交OA,OB于F,E两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
EF长为半径作圆弧,两条圆弧交于点P,作射线OP,过点F作FD∥OB交OP于点D.
(1)若∠OFD=116°,求∠DOB的度数;
(2)若FM⊥OD,垂足为M,求证:△FMO≌△FMD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 轴上两点,其中
轴上两点,其中![]() 与
与![]() 互为相反数.点
互为相反数.点![]() 是第二象限内一点,且
是第二象限内一点,且![]() ,点
,点![]() 是直线
是直线![]() 上一动点;
上一动点;
(1)若![]() ,且
,且![]() 是等腰三角形,求
是等腰三角形,求![]() 的度数;
的度数;
(2)点![]() 在直线
在直线![]() 上运动过程中,当
上运动过程中,当![]() 最短时,求
最短时,求![]() 的大小.
的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知长方形ABCD的两个顶点A(2,﹣1),C(6,2),点M为y轴上一点,△MAB的面积为6.请解答下列问题:
(1)顶点B的坐标 ;
(2)连接BD,求BD的长;
(3)请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
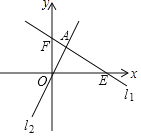
【题目】如图,在平面直角坐标系中,点E的坐标为(4,0),点F的坐标为(0,2),直线11经过点E和点F,直线l1与直线l2:y=2x相交于点A.
(1)求直线l1的表达式;
(2)求点A的坐标;
(3)求△AOE的面积;
(4)当点P是直线l1上的一个动点时,过点P作y轴的平行线PB交直线l2于点B,当线段PB=3时,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列分式方程解应用题
“互联网+”已经成为我们生活中不可或缺的一部分,例如OFO.摩拜等互联网共享单车就为城市短距离出行难提俱了解决方案,小明每天乘坐公交汽车上学,他家与公交站台相距1.2km,现在每天租用共享单车到公交站台所花时间比过去步行少12min,已知小明骑自行车的平均速度是步行平均速度的2.5倍,求小明步行的平均速度是多少km/h?
查看答案和解析>>
科目:初中数学 来源: 题型:
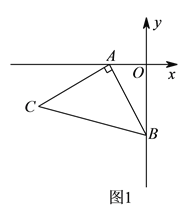
【题目】如图![]() ,
, ![]() ,
, ![]() ,以
,以![]() 点为顶点、
点为顶点、![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() .
.
(![]() )求
)求![]() 点的坐标.
点的坐标.
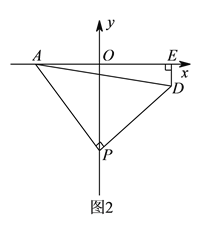
(![]() )如图
)如图![]() ,
, ![]() 为
为![]() 轴负半轴上一个动点,当
轴负半轴上一个动点,当![]() 点沿
点沿![]() 轴负半轴向下运动时,以
轴负半轴向下运动时,以![]() 为顶点,
为顶点, ![]() 为腰作等腰
为腰作等腰![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,求
点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com