
【题目】如图,E、F、G、H分别是四边形ABCD边AB、BC、CD、AD的中点,下列说法正确的是( )
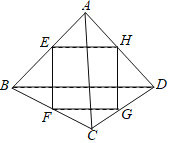
A.当AC⊥BD时,四边形EFGH是菱形
B.当AC=BD时,四边形EFGH是矩形
C.当四边形ABCD是平行四边形时,则四边形EFGH是矩形
D.当四边形ABCD是矩形时,则四边形EFGH是菱形
 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】为了推动我县“三进校园”活动的广泛开展,引导学生走向操场,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)本次调查获取的样本数据的众数为 ,中位数为 ;
(3)根据样本数据,若学校计划购买![]() 双运动鞋,建议购买
双运动鞋,建议购买![]() 号运动鞋 双.
号运动鞋 双.
查看答案和解析>>
科目:初中数学 来源: 题型:
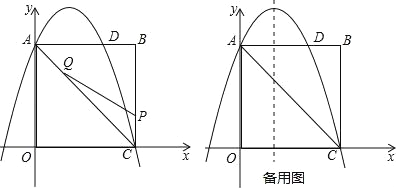
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加射击比赛,两人成绩如图所示.
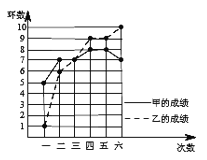
(1)填表:
平均数 | 方差 | 中位数 | 众数 | |
甲 | 7 | 1 | 7 | |
乙 | 9 |
(2)只看平均数和方差,成绩更好的是 .(填“甲”或“乙”)
(3)仅就折线图上两人射击命中环数的走势看,更有潜力的是 .(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(1,4),点B(3,2),连接OA,OB.
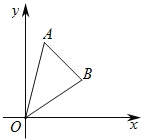
(1)求直线OB与AB的解析式;
(2)求△AOB的面积.
(3)下面两道小题,任选一道作答.作答时,请注明题号,若多做,则按首做题计入总分.
①在y轴上是否存在一点P,使△PAB周长最小.若存在,请直接写出点P坐标;若不存在,请说明理由.
②在平面内是否存在一点C,使以A,O,C,B为顶点的四边形是平行四边形.若存在,请直接写出点C坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
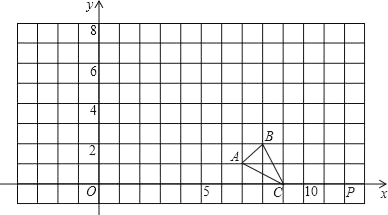
【题目】如图,在直角坐标系中△ABC的A、B、C三点坐标为A(7,1)、B(8,2)、C(9,0).
(1)请在图中画出△ABC的一个以点P(12,0)为位似中心,相似比为3的位似图形△A′B′C′(要求与△ABC同在P点一侧),画出△A′B′C′关于y轴对称的△A′'B′'C′';
(2)写出点A'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C逆时针旋转得到△A′B′C′,M是BC的中点,P是A'B’的中点,连接PM,若BC=4,AC=3,则在旋转的过程中,线段PM的长度不可能是( )
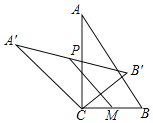
A.5B.4.5C.2.5D.0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m,n,则二次函数![]() 的图象与x轴有两个不同交点的概率是( ).
的图象与x轴有两个不同交点的概率是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(b,-2a).且![]() +|b-l|=0.CD∥AB,AD∥BC
+|b-l|=0.CD∥AB,AD∥BC
(1)直接写出B、C、D各点的坐标:B 、C 、D ;
(2)如图1,P(3,10),点E,M在四边形ABCD的边上,且E在第二象限.若△PEM是以PE为直角边的等腰直角三角形,请直接写出点E的坐标,并对其中一种情况计算说明;
(3)如图2,F为y轴正半轴上一动点,过F的直线j∥x轴,BH平分∠FBA交直线j于点H.G为BF上的点,且∠HGF=∠FAB,F在运动中FG的长度是否发生变化?若变化,求出变化范围;若不变,求出定值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com