
已知二次函数 ,其图像抛物线交
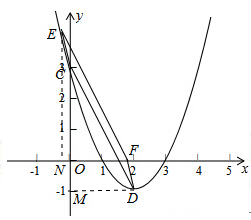
,其图像抛物线交 轴的于点A(1,0)、B(3,0),交y轴于点C.直线
轴的于点A(1,0)、B(3,0),交y轴于点C.直线 过点C,且交抛物线于另一点E(点E不与点A、B重合).
过点C,且交抛物线于另一点E(点E不与点A、B重合).
(1)求此二次函数关系式;
(2)若直线 经过抛物线顶点D,交
经过抛物线顶点D,交 轴于点F,且
轴于点F,且 ∥
∥ ,则以点C、D、E、F为顶点的四边形能否为平行四边形?若能,求出点E的坐标;若不能,请说明理由.
,则以点C、D、E、F为顶点的四边形能否为平行四边形?若能,求出点E的坐标;若不能,请说明理由.
(3)若过点A作AG⊥ 轴,交直线
轴,交直线 于点G,连OG、BE,试证明OG∥BE.
于点G,连OG、BE,试证明OG∥BE.

(1)此二次函数关系式为:y=x2-4x+3;
(2)以点C、D、E、F为顶点的四边形能成为平行四边形;点E的坐标为(2+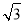 ,2),(2-
,2),(2-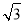 ,2),(2+
,2),(2+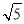 ,4),(2-
,4),(2-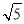 ,4).
,4).
(3)证明见解析.
【解析】
试题分析:(1)由二次函数y=x2+bx+c,其图象抛物线交x轴于点A(1,0),B(3,0),直接利用待定系数法求解即可;
(2)以点C、D、E、F为顶点的四边形构成平行四边形,有两种情形,分类讨论即可;
(3)先过点E作EH⊥x轴于点H,设直线CE的解析式为:y=kx+3,然后分别求得点G与E的坐标,即可证得△OAG∽△BHE,则可得∠AOG=∠HBE,即可.
试题解析:(1)∵二次函数y=x2+bx+c,图象交x轴于点A(1,0),B(3,0),
∴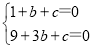 ,
,
解得: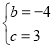 ,
,
∴此二次函数关系式为:y=x2-4x+3;
(2)当CD为平行四边形对角线时,过点D作DM⊥AB于点M,过点E作EN⊥OC于点N,
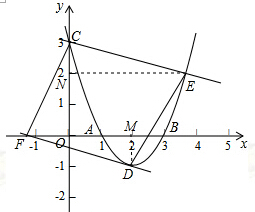
∵y=x2-4x+3=(x-2)2-1,
∴点D(2,-1),点C(0,3),
∴DM=1,
∵l1∥l,
∴当CE=DF时,四边形CEDF是平行四边形,
∴∠ECF+∠CFD=180°,
∵∠OCF+∠OFC=90°,
∴∠ECN+∠DFM=90°,
∵∠DFM+∠FDM=90°,
∴∠ECN=∠FDM,
在△ECN和△FDM中,
 ,
,
∴△ECN≌△FDM(AAS),
∴CN=DM=1,
∴ON=OC-CN=3-1=2,
当y=2时,x2-4x+3=2,
解得:x=2±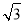 ,
,
∴点E(2+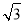 ,2)或(2-
,2)或(2-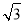 ,2);
,2);
当CD为平行四边形一条边时,
则EF∥CD,且EF=CD.
过点D作DM⊥y轴于点M,则DM=2,OM=1,CM=OM+OC=4;
过点E作EN⊥x轴于点N.
易证△CDM≌△EFN,∴EN=CM=4.
∴x2-4x+3=4,
解得:x=2± .
.
综上所述,以点C、D、E、F为顶点的四边形能成为平行四边形;点E的坐标为(2+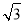 ,2),(2-
,2),(2-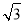 ,2),(2+
,2),(2+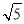 ,4),(2-
,4),(2-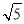 ,4).
,4).
(3)如图,过点E作EH⊥x轴于点H,
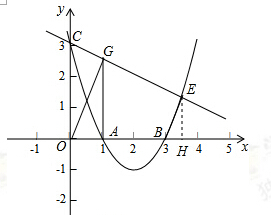
设直线CE的解析式为:y=kx+3,
∵A(1,0),AG⊥x轴,
∴点G(1,k+3),
即OA=1,AG=k+3,
∵E是直线与抛物线的交点,
∴ ,
,
解得: ,
,
∴点E(k+4,(k+1)(k+3)),
∴BH=OH-OB=k+3,EH=(k+1)(k+3),
∴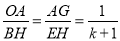 ,
,
∵∠OAG=∠BHE=90°,
∴△OAG∽△BHE,
∴∠AOG=∠HBE,
∴OG∥BE.
考点:二次函数综合题.


科目:初中数学 来源:2014年初中毕业升学考试(江苏镇江卷)数学(解析版) 题型:解答题
如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏镇江卷)数学(解析版) 题型:填空题
一辆货车从甲地匀速驶往乙地,到达后用了半小时卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍.货车离甲地的距离y(千米)关于时间x(小时)的函数图象如图所示.则a= (小时).

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏连云港卷)数学(解析版) 题型:解答题
如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为菱形;
(2)连接AE、BE,AE与BE相等吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏苏州卷)数学(解析版) 题型:解答题
如图,已知函数 (x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(x>0)的图象经过点A,B,点A的坐标为(1,2).过点A作AC∥y轴,AC=1(点C位于点A的下方),过点C作CD∥x轴,与函数的图象交于点D,过点B作BE⊥CD,垂足E在线段CD上,连接OC,OD.
(1)求△OCD的面积;
(2)当BE= AC时,求CE的长.
AC时,求CE的长.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(江苏淮安卷)数学(解析版) 题型:填空题
如图,在四边形ABCD中,AB∥CD,要使得四边形ABCD是平行四边形,应添加的条件是 (只填写一个条件,不使用图形以外的字母和线段).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com